浙江省金华市2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-12-09 类型：期中考试

进入出卷网下载

一、选择题（本题有10小题，每小题3分，共30分）

1. 使用直角尺检验某种工件的凹面，成半圆时为合格．在如图所示的三种情况中，合格的是（）

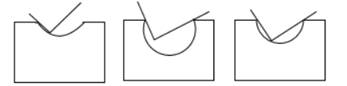A、图1 B、图2 C、图3 D、都不对

查看试题解析
2. 如图是一个游戏转盘，自由转动转盘，当转盘停止转动后，指针落在“Ⅱ”区域内的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{3}$

查看试题解析
3. 若函数 $y = (2 - m) x^{m^{2} - 2} - m x$ 是二次函数，则m的值为（）

A、±2 B、－2 C、2 D、0

查看试题解析
4. 如图，一块直角三角板的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，若⊙O的直径为8，则弦AB的长为（）

A、 $2 \sqrt{2}$ B、 $2 \sqrt{3}$ C、4 D、6

查看试题解析
5. 把函数 $y = {(x - 1)}^{2} + 2$ 的图象向右平移1个单位长度，平移后图象的解析式为（）

A、 $y = x^{2} + 2$ B、 $y = {(x - 1)}^{2} + 1$ C、 $y = {(x - 2)}^{2} + 2$ D、 $y = {(x - 1)}^{2} - 3$

查看试题解析
6. 如图，在正五边形ABCDE中，连结AC，以点A为圆心，AB为半径画弧交AC于点F，连结DF，则∠DFC的度数是（）

A、70° B、72° C、75° D、78°

查看试题解析
7. 在下列语句中，正确的是（）
①相等的圆周角所对的弧相等；②同弧或等弧所对的圆周角相等；③平分弦的直径垂直于弦，并且平分弦所对的弧；④圆的内接平行四边形是矩形．

A、①② B、②③ C、④ D、②④

查看试题解析
8. 2019年10月31日，三大运营商宣布5G商用正式启动，5G时代大步流星地走来．某电器城准备销售一种型号的5G手机，在销售过程中发现，当零售价为每台4000元时，每天可以售出8台，日销售利润为4000元，当零售价每降低50元时，则每天多售出4台，下列结论正确的是（）

A、当零售价每降低200元时，日销售利润最大，最大利润为7200元 B、当零售价每降低100元和零售价每降低300元时，销售数量是一样的 C、手机的进价是每台500元 D、零售价越低，每天售出数量就越多，所以利润就越大

查看试题解析
9. 如图，已知BC是⊙O的直径，OA⊥BC于点O，点D在劣弧AC上（不与点A，C重合），BD与OA交于点E．已知∠AED=65°，则∠AOD=（）

A、40° B、35° C、32.5° D、30°

查看试题解析
10. 如图，已知AC，BD为⊙O的两条直径，连结AB，BC，OE⊥AB于点E，点F是半径OC的中点，连结EF，DF，BF，OB与EF交于点P，若⊙O的半径为1，∠BAC=30°，下列结论错误的是（）

A、 $Δ$ OCB是等边三角形 B、EF= $\frac{\sqrt{3}}{2}$ C、PE=PF D、DF=EF

查看试题解析

二、填空题（本题有6小题，每小题4分，共24分）

11. 抛物线 $y = - x^{2} + 5$ 的顶点坐标是．

查看试题解析

12. 某校为了了解本校九年级男生在“新冠肺炎”疫情期间每天在家进行锻炼的时长情况，随机抽取了100名九年级男生进行问卷调查，将收集到的数据整理如下：

时间x(分钟）	x<10	10≤x<20	20≤x<30	30≤x<40	40≤x<50	50<x<60	x>60
人数	1	8	10	35	21	15	10

根据以上统计结果，随机抽取该校一名九年级男生，估计他每天进行锻炼的时间不少于40分钟的概率是．

查看试题解析

13. 如图，四边形ABCD为⊙O的内接四边形，已知∠A∶∠B∶∠C∶∠D=7∶9∶11∶9，则∠C= ．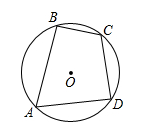

查看试题解析
14. 如图，将一个边长为2的大正方形分成了4个全等的小正方形，阴影部分由3段圆弧围成，大圆弧的半径是2，两个小圆弧的半径都是1，则阴影部分的面积为．

查看试题解析
15. 如图，抛物线 $y = a x^{2} + b x + 1$ 的顶点在直线 $y = k x + 1$ 上，对称轴为直线 $x = 1$ ，以下四个结论：① $a b < 0$ ；② $b < \frac{1}{3}$ ；③ $a = - k$ ；④当 $0 < x < 1$ 其中正确的是．（填序号）

查看试题解析
16. 如图，已知点A的坐标是(6，0)，点C，F分别是直线x=－4与x轴上的动点，CF=10，点D是线段CF的中点，连结AD．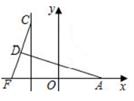

(1)、当点F的坐标是(－4，0)时， $Δ$ ADF的面积为；

(2)、在点C，F运动过程中，AD的取值范围是．

查看试题解析

三、解答题（本题有8小题，共66分）

17. 如图，点A，B，C，D，E都在⊙O上，AC平分∠BAD，且 $\overset{⌢}{A E} = \overset{⌢}{C D}$ ．求证：AB∥CE．

查看试题解析
18. 2020年8月4日，台风“黑格比”来袭，东阳南马镇被雨水“围攻”．如图，当地有一座圆弧形拱桥，跨度AB=60m，拱高PM=18m，当洪水泛滥，水面跨度缩小到30m时要采取紧急措施，当时测量人员测得水面A₁B₁到拱顶距离只有4m时，问是否需要采取紧急措施？请说明理由．

查看试题解析
19. 如图，在单位长度为1的正方形网格中建立平面直角坐标系，一条圆弧经过格点A(0，4)，B(4，4)，C(6，2)三点，请在网格中进行下列操作：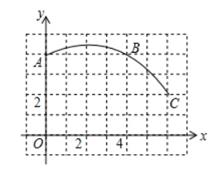

(1)、在图中确定该圆弧所在圆的圆心D的位置，得到点D的坐标是；

(2)、连结AD，CD，求⊙D的半径及的长．

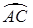查看试题解析
20. 为了了解某班中考体育测试情况，一名同学把本班体育成绩分成四段，A段：0分~29分，B段：30分~39分，C段：40分~49分，D段：50分，并绘制了如下两幅不完整的统计图，请根据统计图提供的信息解答下列问题：

(1)、请补全条形统计图；

(2)、该年级共有学生500人，请根据该班成绩估计该年级成绩在D段的人数；

(3)、如果A，B分数段中各有一名男生，该班教师从A，B分数段中分别任意选出一名同学了解考试中的一些情况，请用列表或画树状图的方法求出所选的两名学生刚好是两名女生的概率．

查看试题解析
21. 如图，已知抛物线 $y = a x^{2} + b x + c$ 经过点A(－1，0)，点B(3，0)和点C(0，3)．

(1)、求抛物线的解析式和顶点E的坐标；

(2)、点C是否在以BE为直径的圆上？请说明理由．

查看试题解析
22. 我们知道求两个函数图象的交点坐标，可以联立两个函数的解析式组成方程组，方程组的解就是交点的坐标．如：求双曲线 $y = \frac{8}{x}$ 与直线 $y = - x + 6$ 的交点坐标，我们可以联立两个解析式得到方程组 ${\begin{cases} y = \frac{8}{x} \\ y = - x + 6 \end{cases}$ ，解得 ${\begin{cases} x_{1} = 4 \\ y_{1} = 2 \end{cases}$ ， ${\begin{cases} x_{2} = 2 \\ y_{2} = 4 \end{cases}$ ，所以双曲线 $y = \frac{8}{x}$ 与直线 $y = - x + 6$ 的交点坐标是(4，2)和(2，4)．已知直线 $y = - x + m$ 和抛物线 $y = x^{2} - 2 x - 3$ ，请利用上述知识解决下列问题：

(1)、当m=－1时，求直线与抛物线的交点坐标．

(2)、当m为何值时，直线与抛物线只有一个交点？

查看试题解析
23. 如图，以 $Δ$ ABC的边AB为直径作⊙O，交BC于点D，交AC于点E，点D为 $\overset{⌢}{B E}$ 的中点．

(1)、判断 $Δ$ ABC的形状，并说明理由；

(2)、连结DE，求证：DE=CD；

(3)、若AB=4，∠BAC=45°，求阴影部分的面积．

查看试题解析
24. 阅读下面材料，并解决问题：

(1)、如图1，等边三角形ABC内有一点P，若点P到顶点A，B，C的距离分别为3，4，5，求∠APB的度数；
为了解决本题，我们可以将 $Δ$ ABP绕顶点A逆时针旋转到 $Δ$ ACP′处，此时 $Δ$ ACP′≌ $Δ$ ABP，这样就可以利用旋转变换，将三条线段PA，PB，PC转化到一个三角形中，从而求出∠APB=；

(2)、基本运用：
请你利用第（1）题的思想方法，解答下面问题：

如图2，在 $Δ$ ABC中，∠CAB=90°，AB=AC，E，F为BC上的点，且∠EAF=45°．求证：EF²=BE²+FC²；

(3)、能力提升：在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB=4．
①如图3，将 $Δ$ ADE绕点D逆时针旋转90°得到 $Δ$ DCF，连结EF．

a．把图形补充完整（无需写画法）；

b．求EF²的取值范围；

②如图4，求BE+AE+DE的最小值．

查看试题解析