浙江省衢州市2020-2021学年八年级上学期数学期中考试试卷

试卷更新日期：2020-12-09 类型：期中考试

进入出卷网下载

一、选择题（本题共有8小题，每小题3分，共24分）

1. 衢州市教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 需要做一个三角形的木架，在以下四组长度的木棒中，符合条件的是（）

A、3cm，2cm，1cm B、3cm，4cm，5cm C、5cm，12cm，6cm D、6cm，6cm，12cm

查看试题解析
3. 不等式组 ${\begin{array}{l} x \leq 1 \\ x > - 3 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 若a<b，则运用不等式性质变形正确的是（）

A、a+4>b+4 B、a－3>b－3 C、 $\frac{1}{2} a > \frac{1}{2} b$ D、－2a>－2b

查看试题解析
5. 如图，已知BC=DC，那么添加下列一个条件后，仍无法判定 $Δ$ ABC≌ $Δ$ ADC的是（）

A、∠B=∠D=90° B、∠BCA=∠DCA C、∠BAC=∠DAC D、AB=AD

查看试题解析
6. 如图，在5×5的方格纸中有一个格点 $Δ$ ABC（每个小正方形的边长为1），下列关于它的描述，正确的是（）

A、面积为7 B、三边长都是有理数 C、是直角三角形 D、是等腰三角形

查看试题解析
7. 已知关于x的不等式组 ${\begin{cases} a - x > 0 \\ 3 x + 5 > 0 \end{cases}$ 的整数解共有4个，则a的取值范围是（）

A、2≤a≤3 B、2<a≤3 C、2≤a<3 D、2<a<3

查看试题解析
8. 如图，在 $Δ$ ABC中，AC=BC，∠ACB=90°，过点C作CD⊥AB交∠CAB的平分线AE于点O，点P是AC延长线上一点，OP=OB，现有下列结论：①∠OCP=∠OEB；②∠POB=90°；③CP=OD；④S_{$Δ$ COP}=S_{$Δ$ COE}；⑤PC²+BC²=OP²+OB² ．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本题共有8小题，每小题3分，共24分）

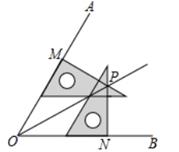
9. 不等式 $3 x + 1 > 7$ 的解集为．

查看试题解析
10. 在Rt $Δ$ ABC中，∠C=90°，∠A－∠B=60°，则∠A= ．

查看试题解析
11. 已知命题“全等三角形的面积相等”，写出它的逆命题．

查看试题解析
12. 两个全等的直角三角尺按如图所示的方式放置，其中两个直角三角尺的短直角边分别在∠AOB的两边上，长直角边交于点P，连结OP，且OM=ON，若∠AOB=60°，OM=6cm，则线段OP=cm．

查看试题解析
13. 如图，点E是Rt $Δ$ ABC、Rt $Δ$ BCD的斜边BC的中点，AB=AC，∠BCD=30°，则∠EAD的度数为．

查看试题解析
14. 关于x的不等式组 ${\begin{cases} 2 x - a > 1 \\ b - 3 x > 0 \end{cases}$ 的解集为 $- 2 < x < 1$ ；则代数式 2019b－4(a+15)³－37的值为.

查看试题解析
15. 如图，在长方形 ABCD中，点E为长方形ABCD的边AD上一点，若AE=2，S_{$Δ$ ABE}=6，将长方形ABCD沿BE折叠，使点A落在EC上的点F处，则 $Δ$ BCE的面积是．

查看试题解析
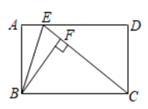16. 如图，等腰 Rt△ABC外有一点D，连结AD、CD，AE垂直平分DC于点E，∠DAB的平分线交DC于点F，连结BF，若 BF=1，AF= 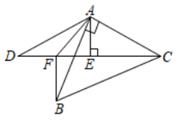$\sqrt{2}$ ，则线段CF= ．

查看试题解析

三、解答题（本题共有7小题，第17~19小题每小题6分，第20~22小题每小题8分，第23小题每小题10分，共52分．）

17. 解下列不等式和不等式组．

(1)、2(x+1)>3x－4；

(2)、 ${\begin{cases} 9 x + 5 < 8 x + 7 \\ \frac{4}{3} x + 2 > 1 - \frac{2}{3} x \end{cases}$

查看试题解析
18. 已知，如图，AB=BC，∠A=∠C．求证：AD=CD．

查看试题解析
19. 如图，在4×5的网格中，小正方形的边长为1，点A，B，C，D均为格点（小正方形的顶点）．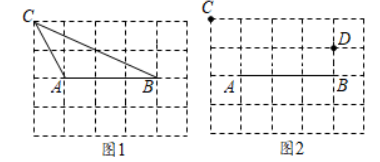

(1)、如图1，画出所有以AB为一边且与 $Δ$ ABC全等的格点三角形；

(2)、如图2，在线段AB上画出一点P，使CP+PD的值最小，并求出最小值．

查看试题解析
20. 如图，在 $Δ$ ABC中，AB=AC=3cm，∠BAC=110°，点D在线段BC上（不与点B、C重合），连结AD，作∠1=∠C，DE交线段AC于点E．

(1)、若∠BAD=30°，求∠EDC的度数．

(2)、当DC等于多少时， $Δ$ ABD≌ $Δ$ DCE？试说明理由．

查看试题解析
21. 我国古代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它是由4个全等的直角三角形与1个小正方形拼成的一个大正方形，已知大正方形的面积为25，小正方形的面积为3．

(1)、如图1，若用a，b表示直角三角形的两条直角边(a<b)求a+b的值；

(2)、如图2，若拼成的大正方形为正方形ABCD，中间的小正方形为正方形EFGH，连结AC，交BG于点P，交DE于点M，求S_{$Δ$ AFP}－S_{$Δ$ CGP}的值．

查看试题解析
22. 2020年，全球爆发新冠肺炎疫情，某洗化日化公司为扩大经营，决定购进8台机器生产洗手液．现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产洗手液的产量如下表所示，经过预算，本次购买机器所耗资金不能超过36万元．

甲

乙

价格（万元/台)

6

4

每台日产量（吨)

15

10

(1)、按该公司要求可以有几种购买方案？请写出所有的购买方案．

(2)、若该公司购进的8台机器的日生产能力不能低于82吨，那么为了节约资金应选择哪种购买方案？

查看试题解析
23. 如图，在 $Δ$ ABC中，AC=BC，∠ACB=120°，AB=6，点D是射线AM上一点（不与A、B两点重合），点D从点A出发，沿射线AM的方向运动，以CD为一边在CD的右侧作 $Δ$ CDE，使CE=CD，∠DCE=∠ACB，连结BE．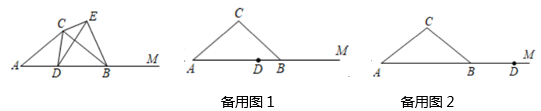

(1)、求∠ABE的度数；

(2)、是否存在以D、E、B为顶点的三角形是直角三角形？若存在，求出线段BD的长；若不存在，请说明理由；

(3)、 $Δ$ BDE的周长是否存在最小值？若存在，求出 $Δ$ BDE的最小周长；若不存在，请说明理由．

查看试题解析

	甲	乙
价格（万元/台)	6	4
每台日产量（吨)	15	10