河南省驻马店市确山县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-12-09 类型:期末考试
一、单选题
-
1. 下列有理数中,最小的数是( )A、 B、0 C、 D、2. 用科学记数法表示中国的陆地面积约为: ,原来的数是 .A、9600000 B、96000000 C、960000 D、960003. 下列说法正确的是( )A、4π是一次单项式 B、 +x﹣3是二次三项式 C、﹣ 的系数是﹣2 D、﹣x的系数是﹣14. 从不同方向观察如图所示的几何体,不可能看到的是( )
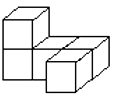 A、
A、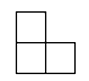 B、
B、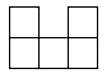 C、
C、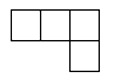 D、
D、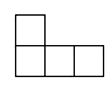 5. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥6. 某家三口准备参加旅行团外出旅行:甲旅行社告知“大人全价,儿童按半价优惠”,乙旅行社告知“家庭旅行可按团体计价,每人均可按全价的八折优惠”,若两家旅行社针对相同项目制订的全价相同,则下列结论成立的是( )A、甲旅行社比乙旅行社优惠 B、乙旅行社比甲旅行社优惠 C、甲旅行社与乙旅行社同样优惠 D、不确定7. 图甲和图乙中所有的正方形都全等,将图甲的正方形放在图乙中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )
5. 不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有8条棱,该模型的形状对应的立体图形可能是( )A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥6. 某家三口准备参加旅行团外出旅行:甲旅行社告知“大人全价,儿童按半价优惠”,乙旅行社告知“家庭旅行可按团体计价,每人均可按全价的八折优惠”,若两家旅行社针对相同项目制订的全价相同,则下列结论成立的是( )A、甲旅行社比乙旅行社优惠 B、乙旅行社比甲旅行社优惠 C、甲旅行社与乙旅行社同样优惠 D、不确定7. 图甲和图乙中所有的正方形都全等,将图甲的正方形放在图乙中的①②③④某一位置,所组成的图形不能围成正方体的位置是( )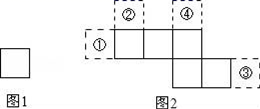 A、① B、② C、③ D、④8. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、9. 如图,长方形纸片 , 为 边的中点,将纸片沿 、 折叠,使点 落在点 处,点 落在点 处,若 ,则 ( )
A、① B、② C、③ D、④8. 中国古代人民很早就在生产生活中发现了许多有趣的数学问题,其中《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有 辆车,则可列方程( )A、 B、 C、 D、9. 如图,长方形纸片 , 为 边的中点,将纸片沿 、 折叠,使点 落在点 处,点 落在点 处,若 ,则 ( ) A、 B、 C、 D、10. 如图,图形中都是由几个灰色和白色的正方形按一定规律组成,第1个图中有2个灰色正方形,第2个图中有5个灰色正方形,第3个图中有8个灰色正方形,第4个图中有11个灰色正方形,…依此规律,第( )个图中灰色正方形的个数是2021.
A、 B、 C、 D、10. 如图,图形中都是由几个灰色和白色的正方形按一定规律组成,第1个图中有2个灰色正方形,第2个图中有5个灰色正方形,第3个图中有8个灰色正方形,第4个图中有11个灰色正方形,…依此规律,第( )个图中灰色正方形的个数是2021. A、673 B、674 C、675 D、676
A、673 B、674 C、675 D、676二、填空题
-
11. 如果关于x的方程 的解是2,那么a的值是.12. 一个角为 ,则它的补角的大小为.13. 边长分别为a和2a的两个正方形按如图的样式摆放,则图中阴影部分的面积为.
 14. 以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,则∠AOP的度数为.15. 已知a,b互为相反数,c,d互为倒数, .则代数式(a+b+1)x2+cdy2+x2y-xy2的值是.
14. 以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,则∠AOP的度数为.15. 已知a,b互为相反数,c,d互为倒数, .则代数式(a+b+1)x2+cdy2+x2y-xy2的值是.三、解答题
-
16. 计算:(1)、 ;(2)、 ;(3)、 .17. 解方程: +1=x﹣ .18. 先化简,再求值: ,其中 , 满足 .19. 阅读材料:
我们知道, ,类似地,我们把 看成一个整体,则 = .“整体思想”是初中数学解题中的一种重要的思想方法,它在多项式的化简与求职中应用极为广泛.
尝试应用:
(1)、把 看成一个整体,合并 的结果为.(2)、已知 ,求 的值.(3)、已知 ,求 的值.20. 如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“ ”形中的5个数字的最小数为a.
(1)、请用含a的代数式表示这5个数;(2)、这五个数的和与“ ”形中心的数有什么关系?(3)、盖住的5个数字的和能为105吗?为什么?21. 线段和角是我们初中数学常见的平面几何图形,它们的表示方法、和差计算以及线段的中点、角的平分线的概念等有很多相似之处,所以研究线段或角的问题时可以运用类比的方法.
特例感知:
(1)、如图1,已知点 是线段 的中点,点 是线段 的中点若 , ,则线段 ;(2)、如图1,已知点 是线段 的中点,点 是线段 的中点,若 , ,则求线段 的长;(3)、如图2, 平分 , 平分 ,设 , ,请直接用含 的式子表示 的大小.22. 七年级(1)班的全体同学排成一列步行去市博物馆参加科技活动,小涛担任通讯员.在队伍中,小涛先数了一下他前后的人数,发现前面的人数是后面人数的2倍,他往前超了8名同学后,发现前面的人数和后面的人数一样.(1)、七年级(1)班有多少名同学?(2)、这些同学要过一座长60米的大桥,安全起见,相邻两个同学间保持相同的固定距离,队伍前进速度为1.2米/秒,从第一名同学刚上桥到全体通过大桥用了90秒,则队伍的全长为多少米?(3)、在(2)的条件下,排在队尾的小刚想把一则通知送到队伍最前的小婷手中,若小刚从队尾追赶小婷的速度是4.2米/秒,他能在15秒内追上小婷吗?说明你的理由.23. 如图,在数轴上点 对应的数为 ,点 对应的数为8,点 对应的数为 , 为原点. (1)、 两点的距离是;(2)、若点 以每秒5个单位长度的速度沿数轴正方向运动,则2秒时 , 两点的距离是;(3)、若点 都以每秒4个单位长度的速度沿数轴正方向运动,而点 不动, 秒时, 中有一点是三点所在线段的中点,求 的值.
(1)、 两点的距离是;(2)、若点 以每秒5个单位长度的速度沿数轴正方向运动,则2秒时 , 两点的距离是;(3)、若点 都以每秒4个单位长度的速度沿数轴正方向运动,而点 不动, 秒时, 中有一点是三点所在线段的中点,求 的值.