河南省信阳市潢川县2019-2020学年七年级上学期数学期末考试试卷(B卷)
试卷更新日期:2020-12-09 类型:期末考试
一、单选题
-
1. 的相反数是( )A、 B、2 C、 D、2. 有理数a,b,c,d在数轴上的对应点的位置如图所示,则正确的结论是( )
 A、a>﹣4 B、bd>0 C、|a|>|b| D、b+c>03. 若k袋苹果重m千克,则x袋苹果重( )千克.A、 B、 C、 D、4. 下列语句正确的是( )A、近似数0.010精确到百分位 B、|x-y|=|y-x| C、如果两个角互补,那么一个是锐角,一个是钝角 D、若线段AP=BP,则P一定是AB中点5. 如图,如果用剪刀沿直线将一个正方形图片剪掉一部分,发现剩下部分的周长比原正方形图片的周长要小,能正确解释这一现象的数学知识是( )
A、a>﹣4 B、bd>0 C、|a|>|b| D、b+c>03. 若k袋苹果重m千克,则x袋苹果重( )千克.A、 B、 C、 D、4. 下列语句正确的是( )A、近似数0.010精确到百分位 B、|x-y|=|y-x| C、如果两个角互补,那么一个是锐角,一个是钝角 D、若线段AP=BP,则P一定是AB中点5. 如图,如果用剪刀沿直线将一个正方形图片剪掉一部分,发现剩下部分的周长比原正方形图片的周长要小,能正确解释这一现象的数学知识是( ) A、线段比曲线短 B、经过一点有无数条直线 C、经过两点,有且仅有一条直线 D、两点之间,线段最短6. 下列各组单项式:①ab2与a2b;②2a与a2;③2x2y与-3yx2;④3x与 ,其中是同类项的有( )组.A、0 B、1 C、2 D、37. 如图,O是直线AB上一点,OC平分∠DOB,∠COD=55°45′,则∠AOD=( )
A、线段比曲线短 B、经过一点有无数条直线 C、经过两点,有且仅有一条直线 D、两点之间,线段最短6. 下列各组单项式:①ab2与a2b;②2a与a2;③2x2y与-3yx2;④3x与 ,其中是同类项的有( )组.A、0 B、1 C、2 D、37. 如图,O是直线AB上一点,OC平分∠DOB,∠COD=55°45′,则∠AOD=( ) A、68°30′ B、69°30′ C、68°38′ D、69°38′8. 如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是
A、68°30′ B、69°30′ C、68°38′ D、69°38′8. 如下图,将直角三角形绕一条边所在直线旋转一周后形成的几何体不可能是 A、
A、 B、
B、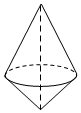 C、
C、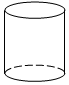 D、
D、 9. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、10. 下列卡片上的数,按照一定的规律排列,依此规律,第300个卡片上的数是( )
9. 我国明代珠算家程大位的名著《直指算法统宗》里有一道著名算题:”一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?”意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,试问大、小和尚各多少人?设大和尚有x人,依题意列方程得( )A、 =100 B、 =100 C、 D、10. 下列卡片上的数,按照一定的规律排列,依此规律,第300个卡片上的数是( ) A、904 B、901 C、895 D、898
A、904 B、901 C、895 D、898二、填空题
-
11. 近似数2.30万精确到位,用科学记数法表示为.12. 已知∠ =34°47′,则它的余角与它的补角之和为.13. 一个两位数的个位上的数字是1,十位上的数字比个位上的数字大a,则这个两位数是.14. 一商店,将某品牌西服先按原价提高 ,然后在广告中写上“大酬宾,八折优惠”,结果每套西服比原价多赚160元,那么每套西服的原价为.15. 从12点整开始到1点,经过分钟,钟表上时针和分针的夹角恰好为99°.
三、解答题
-
16. 计算:(1)、 ;(2)、17. 先化简,再求值:(2x2﹣2y2)﹣3(x2y2+x2)+3(x2y2+y2),其中x=﹣1,y=2.18. 解方程:(1)、9y﹣2(﹣y+4)=3(2)、 .19. 根据要求画图

( 1 )画线段BC;
( 2 )画∠ADB;
( 3 )线段BA的延长线与线段CD的反向延长线相交于点O
20. 学校田径队的张翔在400米跑测试时,先以6米/秒的速度跑完大部分路程,最后以8米/秒的速度冲刺到达终点,成绩为1分3秒,问张翔在离终点处多远时开始冲刺?21. 如图,点B在线段AC的延长线上,AC<CB,点M、N分别是AC、BC的中点,点D是AB的中点. (1)、若AC=8cm,CB=10cm,求线段MN的长;(2)、若AC=a,CB=b,求线段CD的长.22. 为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:
(1)、若AC=8cm,CB=10cm,求线段MN的长;(2)、若AC=a,CB=b,求线段CD的长.22. 为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数据,回答:月份
一
二
三
四
用水量(吨)
16
18
30
35
水费(元)
32
36
65
80
(1)、a=;b=;(2)、若小明家五月份用水32吨,则应缴水费元;(3)、若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?23. 如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.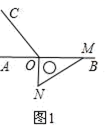 (1)、将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:射线ON是否平分∠AOC?请说明理由;
(1)、将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:射线ON是否平分∠AOC?请说明理由; (2)、将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转至图3,使射线ON恰好平分锐角∠AOC,求此时旋转一共用了多少时间?
(2)、将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转至图3,使射线ON恰好平分锐角∠AOC,求此时旋转一共用了多少时间? (3)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
(3)、将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.