初中数学苏科版2020-2021学年七年级上学期期末模拟试卷
试卷更新日期:2020-12-08 类型:期末考试
一、单选题
-
1. 如果零上3℃记作 +3℃,那么零下5℃记作( )A、-5 B、5 C、-5℃ D、5℃2. 下列各对数中互为相反数的是A、 与 B、 与 C、 与 D、 与3. 如下图是一个数值运算程序,当输入值为-2时,则输出的数值为_____________
 A、3 B、8 C、64 D、634. 如图,是一个正方体,它的展开图是下列四个展开图中的( )
A、3 B、8 C、64 D、634. 如图,是一个正方体,它的展开图是下列四个展开图中的( )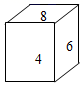 A、
A、 B、
B、 C、
C、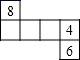 D、
D、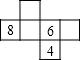 5. 多项式8x2-3x+5与多项式3x3+2mx2-5x+7相加后,不含二次项,则常数m的值是( )A、2 B、-4 C、-2 D、-86. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为( )
5. 多项式8x2-3x+5与多项式3x3+2mx2-5x+7相加后,不含二次项,则常数m的值是( )A、2 B、-4 C、-2 D、-86. 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为( )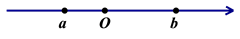 A、3b B、2a +b C、-2a-b D、b7. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确是( )A、 B、 C、 D、8. 如图∠AOC=∠BOD= ,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:图中小于平角的角有6个;丙:∠AOB+∠COD = ;丁:∠BOC+∠AOD = .其中正确的结论有( ).
A、3b B、2a +b C、-2a-b D、b7. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确是( )A、 B、 C、 D、8. 如图∠AOC=∠BOD= ,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:图中小于平角的角有6个;丙:∠AOB+∠COD = ;丁:∠BOC+∠AOD = .其中正确的结论有( ).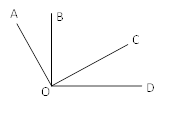 A、4个 B、3个 C、2个 D、1个9. 2017减去它的 ,再减去余下的 ,再减去余下的 ,…依次类推,一直减到余下的 ,则最后剩下的数是( )A、 B、 C、 D、10. 三味书屋推出售书优惠方案:(1)一次性购书不超过100元,不享受优惠;(2)一次性购书超过100元但不超过200元一律打九折;(3)一次性购书超过200元及以上一律打八折。如果王明同学一次性购书162元,那么王明所购书的原价一定为 ( )
A、4个 B、3个 C、2个 D、1个9. 2017减去它的 ,再减去余下的 ,再减去余下的 ,…依次类推,一直减到余下的 ,则最后剩下的数是( )A、 B、 C、 D、10. 三味书屋推出售书优惠方案:(1)一次性购书不超过100元,不享受优惠;(2)一次性购书超过100元但不超过200元一律打九折;(3)一次性购书超过200元及以上一律打八折。如果王明同学一次性购书162元,那么王明所购书的原价一定为 ( )
A、180元 B、202.5元 C、180元或202.5元 D、180元或200元二、填空题
-
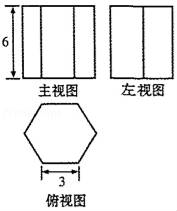
11. 新型冠状病毒蔓延全球,截至北京时间2020年6月20日,全球新冠肺炎累计确诊病例超过8500000例,这个数字用科学记数法表示为。12. 一个角的补角等于这个角的余角的4倍,这个角是.13. 若 ,则 的值为.14. 某同学在做计算2A+B时,误将“2A+B”看成了“2A﹣B”,求得的结果是9x2﹣2x+7,已知B=x2+3x+2,则2A+B的正确答案为 .15. 已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的侧面积为.
 16. 足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分. 初三.(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了场.17. 若规定“!”是一种数学运算符号,且 则 的值为18. 如图,AB=20cm,AO=PO=2cm,∠POQ=60°,现点P绕着点O以30°/s的速度顺时针旋转一周后停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点也能相遇,则点Q运动的速度为cm/s
16. 足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分. 初三.(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了场.17. 若规定“!”是一种数学运算符号,且 则 的值为18. 如图,AB=20cm,AO=PO=2cm,∠POQ=60°,现点P绕着点O以30°/s的速度顺时针旋转一周后停止,同时点Q沿直线BA自B点向A点运动,假若点P、Q两点也能相遇,则点Q运动的速度为cm/s
三、解答题
-
19. 计算(1)、(2)、-14-(1-0.4)÷×[(-2)2-6]20. 解方程(1)、 x=8- (20-x)(2)、21. 已知:有理数m所表示的点与﹣1表示的点距离4个单位,a,b 互为相反数,且都不为零,c,d互为倒数.求:2a+2b+( ﹣3cd)﹣m的值.22. 在做解方程练习时,有一个方程“ ”题中∎处不清晰,李明问老师,老师只是说:“∎是一个有理数,该方程的解与当X=3时的整式 的值相同。”依据老师的提示,请你帮李明求出方程的解,并找到这个有理数。23. 用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.如:1☆3=1×32+2×1×3+1=16.(1)、求 ☆3;(2)、若2☆x=m, ☆3=n(其中x为有理数),试比较m,n的大小.24. 如图,数轴上点A表示的数为6,点B位于A点的左侧,AB=10,动点P从点A出发,以每秒3个单位长度的速度沿数轴向左运动,动点Q从点B出发,以每秒2个单位长度的速度沿数轴向右运动.
 (1)、点B表示的数是;(2)、若点P,Q同时出发,求:
(1)、点B表示的数是;(2)、若点P,Q同时出发,求:①当点P与Q相遇时,它们运动了多少秒?相遇点对应的数是多少?
②当PQ=5个单位长度时,它们运动了多少秒?
25. 2019年10月第二届换广西公路自行车世界巡回赛开赛,有来自世界各地的多支顶级车队参赛,在本次赛事上,组委会把若干翻译志愿者分配给各车队.若毎支车队分配3人,则多出10人,若每支车队分配4人,则还缺8人.(1)、请问一共有几支车队参赛?(2)、组委会给每位参赛车手提供两张号码布和一个电子计时芯片,现有两家供应商提供了如下报价:①若有a名选手参赛,请用含a的式子分别表示甲、乙两家供应商所需的费用;
②请你通过计算说明组委会会选择哪个供应商比较省钱.
 26. 在三角形AOB和三角形COD中,∠AOB=∠COD ,
26. 在三角形AOB和三角形COD中,∠AOB=∠COD ,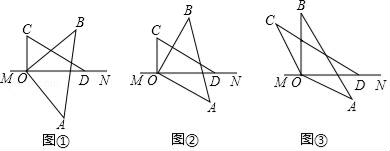 (1)、已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.(2)、已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.(3)、当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD .
(1)、已知∠AOB=90°,把两个三角形拼成如图①所示的图案,当∠BOD=30°时,求∠AOC的度数.(2)、已知∠AOB=90°,把两个三角形拼成如图②所示的图案,当∠AOC=2∠BOD时,求∠BOD的度数.(3)、当∠AOB=α时,把两个三角形拼成如图③所示的图案.用含有α的代数式表示∠AOC+∠BOD .