陕西省宝鸡市陇县2021届九年级上学期数学期中联考试卷

试卷更新日期：2020-12-08 类型：期中考试

进入出卷网下载

一、单选题

1. 已知关于x的方程 $(m + 1) x^{2} - 3 = 0$ 是一元二次方程，则m的取值范围是（）

A、 $m > － 1$ B、 $m \neq 0$ C、 $m \leq － 1$ D、 $m \neq － 1$

查看试题解析
2. 二次函数y＝x²+2x-4的顶点坐标为（）

A、（1，5） B、（-1，5） C、（-1，-5） D、（1 ，-5）

查看试题解析
3. 已知 $x = 1$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} = 0$ 的一个根，则m的值为（）

A、-1或2 B、-1 C、2 D、0

查看试题解析
4. 关于二次函数 $y = 2 x^{2} + 4 x - 1$ ，下列说法正确的是（）

A、图象与y轴的交点坐标为 $(0 ， 1)$ B、图象的对称轴在y轴的右侧 C、当 $x < 0$ 时，y的值随x值的增大而减小 D、y的最小值为-3

查看试题解析
5. 若一元二次方程2x²-（a+1）x＝x（x-1）-1化成一般形式后，二次项系数与一次项系数互为相反数.则a的值为（　　）

A、-1 B、1 C、-2 D、2

查看试题解析
6. 将抛物线 $y = 2 {(x - 3)}^{2} + 2$ 向左平移3个单位长度，再向下平移2个单位长度，得到抛物线的解析式是（）

A、 $y = 2 {(x - 6)}^{2}$ B、 $y = 2 {(x - 6)}^{2} + 4$ C、 $y = 2 x^{2}$ D、 $y = 2 x^{2} + 4$

查看试题解析
7. 关于x的一元二次方程（m-2）x²+3x-1＝0有实数根，那么m的取值范围是（　　）

A、m≤ $\frac{1}{4}$ B、m≥ $- \frac{1}{4}$ 且m≠2 C、m≤ $- \frac{1}{4}$ 且m≠﹣2 D、m≥ $- \frac{1}{4}$

查看试题解析
8. 已知二次函数 $y = x^{2} - 2 b x + 2 b^{2} - 4 c$ （其中x是自变量）的图象经过不同两点A（1-b，m），B（2b+c，m），且该二次函数的图象与x轴有公共点，则b+c的值（）

A、3 B、2 C、1 D、-1

查看试题解析
9. 用配方法解方程 $2 x^{2} + 3 = 7 x$ 时，方程可变形为（）

A、 ${(x - \frac{7}{2})}^{2} = \frac{37}{4}$ B、 ${(x - \frac{7}{2})}^{2} = \frac{43}{4}$ C、 ${(x - \frac{7}{4})}^{2} = \frac{1}{16}$ D、 ${(x - \frac{7}{4})}^{2} = \frac{25}{16}$

查看试题解析
10. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于 $A ， B$ 两点，其对称轴与x轴交于点C，其中 $A ， C$ 两点的横坐标分别为 $- 1$ 和 $1 ，$ 下列说法错误的是（）

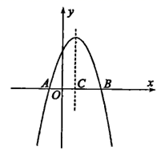A、 $a b c < 0$ B、 $4 a + c = 0$ C、 $16 a + 4 b + c < 0$ D、当 $x > 2$ 时，y随x的增大而减小

查看试题解析

二、填空题

11. 方程 ${(x - 1)}^{2} = 16$ 的根是.

查看试题解析
12. 二次函数y＝﹣ $\frac{1}{2} x^{2}$ ﹣4x+5的图象的对称轴是直线x＝.

查看试题解析
13. 关于x的方程（a-5）x²-4x-1＝0没有实数根，则a满足的条件是.

查看试题解析
14. 已知两点A（-5，y₁），B（3，y₂）均在抛物线y=ax²＋bx＋c（a≠0）上，点C（x₀ ， y₀）是该抛物线的顶点.若y₁＞y₂≥y₀ ，则x₀的取值范围是.

查看试题解析

三、解答题

15. 已知抛物线y=a(x-h)² ，当x=2时，有最大值，此抛物线过点(1，-3)，求抛物线的解析式，并指出当x为何值时，y随x的增大而减小.

查看试题解析
16. 用指定方法解方程：

(1)、2x²-5x-7＝0；（配方法）

(2)、2x²＝2x+1.（公式法）

查看试题解析
17. 已知二次函数y＝ax²+bx﹣3的图象经过点（1，﹣4）和（﹣1，0）．

(1)、求这个二次函数的表达式；

(2)、x在什么范围内，y随x增大而减小？该函数有最大值还是有最小值？求出这个最值．

查看试题解析
18. 若关于x的一元二次方程x²-3x+a-2＝0有实数根.

(1)、求a的取值范围；

(2)、当a为符合条件的最大整数，求此时方程的解.

查看试题解析
19. 如图，已知二次函数 $y = - \frac{1}{2} x^{2} + b x + c$ 的图象经过 $A (2 ， 0)$ ， $B (0 ， - 6)$ 两点.

(1)、求这个二次函数的解析式；

(2)、设该二次函数的对称轴与 $x$ 轴交于点 $C$ ，连接 $B A$ ， $B C$ ，求 $Δ A B C$ 的面积.

查看试题解析
20. 已知关于x的方程x²-（m+1）x+2（m-1）=0.若等腰三角形一边长为4，另两边恰好是此方程的根，求此三角形的另两边长.

查看试题解析
21. 小张2019年末开了一家商店，受疫情影响，2020年4月份才开始盈利，4月份盈利6000元，6月份盈利达到7260元，且从4月份到6月份，每月盈利的平均增长率都相同.

(1)、求每月盈利的平均增长率.

(2)、按照这个平均增长率，预计2020年7月份这家商店的盈利将达到多少元？

查看试题解析
22. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 2$ 交x轴于A，B两点，交y轴于点C，且 $O A = 2 O C = 8 O B$ ，点P是第三象限内抛物线上的一动点.

(1)、求此抛物线的表达式；

(2)、若 $P C / / A B$ ，求点P的坐标；

(3)、连接 $A C$ ，求 $Δ P A C$ 面积的最大值及此时点P的坐标.

查看试题解析