甘肃省白银市会宁县2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-08 类型:期中考试
一、单选题
-
1. 方程 的解是( )A、 B、 C、 , D、2. 上海世博会的某纪念品原价150元,连续两次涨价a%后售价为216元.下列所列方程中正确的是( )A、150(1+2a%)=216 B、150(1+a%)2=216 C、150(1+a%)×2=216 D、150(1+a%)+150(1+a%)2=2163. 下列命题中,真命题是( )A、两条对角线垂直的四边形是菱形 B、对角线垂直且相等的四边形是正方形 C、两条对角线相等的四边形是矩形 D、两条对角线相等的平行四边形是矩形4. 从等腰三角形、平行四边形、菱形、角、线段中随机抽取两个,得到的都是中心对称图形的概率是( )A、 B、 C、 D、5. 把方程 x2﹣x﹣5=0,化成(x+m)2=n的形式得( )A、(x﹣ )2= B、(x﹣ )2= C、(x﹣ )2= D、(x﹣ )2=6. 菱形ABCD的一条对角线长为6cm,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长等于( )A、10cm B、12 cm C、16cm D、12cm或16cm7.
如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
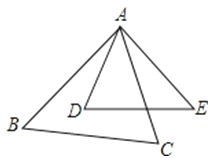 A、= B、= C、= D、=8. 如图,四边形ABCD为菱形,则下列描述不一定正确的是( )
A、= B、= C、= D、=8. 如图,四边形ABCD为菱形,则下列描述不一定正确的是( )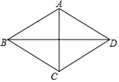 A、CA平分∠BCD B、AC,BD互相平分 C、AC=CD D、∠ABD+∠ACD=90°9. 已知一元二次方程 的两个实数根分别是 x1 、 x2 则 x12 x2 + x1 x22 的值为( )A、-6 B、- 3 C、3 D、610. 如图,正方形ABCD中,点E是AD边的中点,BD , CE交于点H , BE、AH交于点G , 则下列结论:
A、CA平分∠BCD B、AC,BD互相平分 C、AC=CD D、∠ABD+∠ACD=90°9. 已知一元二次方程 的两个实数根分别是 x1 、 x2 则 x12 x2 + x1 x22 的值为( )A、-6 B、- 3 C、3 D、610. 如图,正方形ABCD中,点E是AD边的中点,BD , CE交于点H , BE、AH交于点G , 则下列结论:①∠ABE=∠DCE;②∠AHB=∠EHD;③S△BHE=S△CHD;④AG⊥BE . 其中正确的是( )
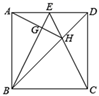 A、①③ B、①②③④ C、①②③ D、①③④
A、①③ B、①②③④ C、①②③ D、①③④二、填空题
-
11. 如图,在菱形ABCD中, ,对角线 ,则菱形ABCD的面积为.
 12. 方程(x-3)2=x-3的根是.13.
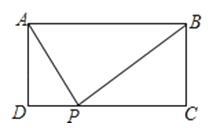
12. 方程(x-3)2=x-3的根是.13.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP= .
 14. 已知x1 , x2是方程x2+3x+1=0的两实数根,则 的值为.15. 如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF=.
14. 已知x1 , x2是方程x2+3x+1=0的两实数根,则 的值为.15. 如图,a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F.若AB=2,CB=4,DE=3,则EF=.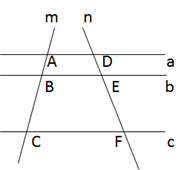 16. 已知 (x、y、z均不为零),则 .17. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,则P点的坐标为.
16. 已知 (x、y、z均不为零),则 .17. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,则P点的坐标为.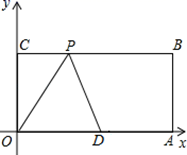 18. 对于实数a,b,定义运算“ ”, 例如 ,因为 ,所以 .若 是一元二次方程 的两个根,则 .
18. 对于实数a,b,定义运算“ ”, 例如 ,因为 ,所以 .若 是一元二次方程 的两个根,则 .三、解答题
-
19. 解方程(用指定方法解下列方程):(1)、 (配方法)(2)、 (公式法)20. 如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
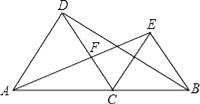 (1)、求证:△ACE≌△DCB;(2)、求证:△ADF∽△BAD.
(1)、求证:△ACE≌△DCB;(2)、求证:△ADF∽△BAD.
21. 已知:关于x的方程x2-4mx+4m2-1=0.(1)、不解方程,判断方程的根的情况;(2)、若△ABC为等腰三角形,BC=5,另外两条边是方程的根,求此三角形的周长.22. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为 万元/辆,经销一段时间后发现:当该型号汽车售价定为 万元/辆时,平均每周售出 辆;售价每降低 万元,平均每周多售出 辆.(1)、当售价为 万元/辆时,平均每周的销售利润为万元;(2)、若该店计划平均每周的销售利润是 万元,为了尽快减少库存,求每辆汽车的售价.23. 如图,在平行四边形ABCD中,过点A作AE垂直BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B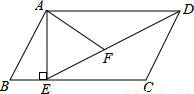 (1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6,AF=4,求AE的长.24. 某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)、求证:△ADF∽△DEC;(2)、若AB=8,AD=6,AF=4,求AE的长.24. 某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题: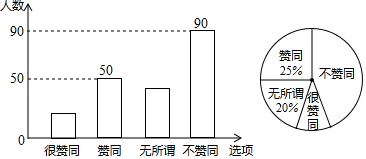 (1)、本次共调查了名家长;扇形统计图中“很赞同”所对应的圆心角是度.已知该校共有1600名家长,则“不赞同”的家长约有名;请补全条形统计图;(2)、从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.25. 如图,在▱BCFD中,点E是DF的中点,连接CE并延长,与BD的延长线相交于点A,连接CD,AF.
(1)、本次共调查了名家长;扇形统计图中“很赞同”所对应的圆心角是度.已知该校共有1600名家长,则“不赞同”的家长约有名;请补全条形统计图;(2)、从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.25. 如图,在▱BCFD中,点E是DF的中点,连接CE并延长,与BD的延长线相交于点A,连接CD,AF.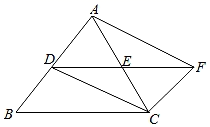 (1)、求证:四边形ADCF是平行四边形;(2)、若CA=CB,则▱ ADCF为(填矩形、菱形、正方形中的一个).26. 如图,在△ABC中,∠C=90°,AC=8cm , BC=6cm , 点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.
(1)、求证:四边形ADCF是平行四边形;(2)、若CA=CB,则▱ ADCF为(填矩形、菱形、正方形中的一个).26. 如图,在△ABC中,∠C=90°,AC=8cm , BC=6cm , 点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.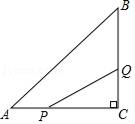 (1)、若P、Q同时出发,经过几秒钟S△PCQ=2cm2;(2)、若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.27. 已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)、若P、Q同时出发,经过几秒钟S△PCQ=2cm2;(2)、若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.27. 已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.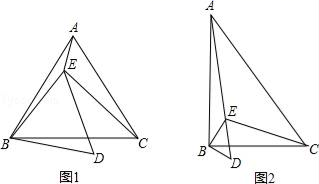 (1)、当α=60°时(如图1),
(1)、当α=60°时(如图1),①判断△ABC的形状,并说明理由;
②求证:BD= AE;
(2)、当α=90°时(如图2),求 的值.28. 正方形ABCD中,点O是对角线AC的中点,P是对角线AC上一动点,过点P作PF⊥CD于点F.如图1,当点P与点O重合时,显然有DF=CF.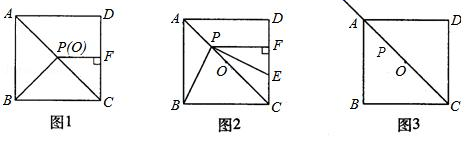 (1)、如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E.
(1)、如图2,若点P在线段AO上(不与点A、O重合),PE⊥PB且PE交CD于点E.①求证:DF=EF;
②写出线段PC、PA、CE之间的一个等量关系;并说出理由;
(2)、若点P在线段OC上(不与点O、C重合),PE⊥PB且PE交直线CD于点E.请完成图3并判断(1)中的结论①、②是否分别成立?若不成立,写出相应的结论.(所写结论均不必证明)