河南省许昌市襄城县2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-12-08 类型:期末考试
一、单选题
-
1. 2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为( )A、0.1776×103 B、1.776×102 C、1.776×103 D、17.76×1022. 下列各式中,与3x2y3是同类项的是( )
A、 B、 C、 D、3. 如图,点Q的方向是位于点O( ).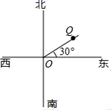 A、北偏东30° B、北偏东60° C、南偏东30° D、南偏东60°4. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、
A、北偏东30° B、北偏东60° C、南偏东30° D、南偏东60°4. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、 B、
B、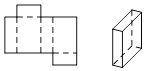 C、
C、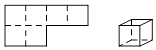 D、
D、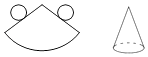 5. 如果a=b,则下列式子不一定成立的是( )A、a+1=b+1 B、 = C、a2=b2 D、a﹣c=c﹣b6. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、7. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、48. 若|a+ |+(b﹣2)2=0,则(ab)2019=( ).A、2019 B、-2019 C、1 D、-19. 如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE= ∠EOC,则下列四个结论正确的个数有( )
5. 如果a=b,则下列式子不一定成立的是( )A、a+1=b+1 B、 = C、a2=b2 D、a﹣c=c﹣b6. 《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设合伙人数为 人,所列方程正确的是( )A、 B、 C、 D、7. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、48. 若|a+ |+(b﹣2)2=0,则(ab)2019=( ).A、2019 B、-2019 C、1 D、-19. 如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,且∠DOE=60°,∠BOE= ∠EOC,则下列四个结论正确的个数有( )①∠BOD=30°;②射线OE平分∠AOC;③图中与∠BOE互余的角有2个;④图中互补的角有6对.
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 是次单项式.11. 某地某天早晨的气温是 ℃,到中午升高了 ℃,晚上又降低了 ℃.那么晚上的温度是 .12. 如图,数轴上A、B两点所表示的数分别是-4和2, 点C是线段AB的中点,则点C所表示的数是.
 13. 如果∠α=35°,那么∠α的余角等于°.14. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是.
13. 如果∠α=35°,那么∠α的余角等于°.14. 已知两个角的和是67°56′,差是12°40′,则这两个角的度数分别是.三、解答题
-
15. 计算(1)、12﹣(﹣18)+(﹣7)﹣15;(2)、﹣42﹣(﹣1)10×|﹣3|÷16. 如图,已知三点A、B、C.
 (1)、请读下列语句,并分别画出图形
(1)、请读下列语句,并分别画出图形画直线AB;画射线AC;连接BC.
(2)、在(1)的条件下,图中共有条射线.(3)、从点C到点B的最短路径是 , 依据是.17. 解方程(1)、4x﹣3=﹣4;(2)、18. 先化简,再求值: 其中19. 如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm. (1)、制作这样的包装盒需要多少平方厘米的硬纸板?(2)、若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)20. 某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.
(1)、制作这样的包装盒需要多少平方厘米的硬纸板?(2)、若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)20. 某校学生会为积极响应武汉市文明创建活动,组织有关方面的知识竞赛,共设有20道选择题,各题分值相同,每题必答,下表记录了3个参赛者的得分情况.参赛者
答对题数
答错题数
得分
A
20
0
100
B
19
1
94
C
18
2
88
(1)、设答对一题记a分,答错一题记b分,则a= , b=;(2)、参赛者E说他得了80分,你认为可能吗,为什么?
