河南省商丘市梁园区2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-12-08 类型：期末考试

进入出卷网下载

一、单选题

1. 便利店售货员小海把“收入100元”记作+100元，那么“-60元”表示（）

A、支出40元 B、支出60元 C、收人40元 D、收入60元

查看试题解析
2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4400000000，这个数用科学记数法表示（）

A、44×10⁷ B、4.4×10⁸ C、4.4×10⁹ D、4.4×10¹⁰

查看试题解析
3. 如图是由5个大小相同的正方体组合而成的几何体，从正面看得到的图形是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 a + 2 b = 5 a b$ B、 $3 a - (- 2 a) = 5 a$ C、 $3 a^{2} - 2 a = a$ D、 $(3 - a) - (2 - a) = 1 - 2 a$

查看试题解析
5. 若一个锐角的余角比这个角大 $30^{\circ}$ ，则这个锐角的补角是（）

A、 $30^{\circ}$ B、 $60^{\circ}$ C、 $150^{\circ}$ D、 $155^{\circ}$

查看试题解析
6. 已知单项式 $2 x^{3} y^{1 + 2 m}$ 与 $3 x^{n + 1} y^{3}$ 的和是单项式，则 $m + n$ 的值是（）

A、3 B、-3 C、6 D、-6

查看试题解析
7. 方程 $\frac{2 x - 1}{4} = 1 - \frac{3 - x}{8}$ 去分母后正确的结果是（）

A、 $2 （ 2 x - 1 ） = 1 - （ 3 - x ）$ B、 $2 （ 2 x - 1 ） = 8 - （ 3 - x ）$ C、 $2 x - 1 = 8 - （ 3 - x ）$ D、 $2 x - 1 = 1 - （ 3 - x ）$

查看试题解析
8. 有理数a，b在数轴上的对应点的位置如图所示，则下列各式成立的是（）

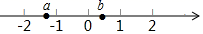A、a＞b B、﹣ab＜0 C、|a|＜|b| D、a＜﹣b

查看试题解析
9. 如图，∠AOB是直角，OA平分∠COD，OE平分∠BOD，若∠BOE=23°，则∠BOC的度数是（）

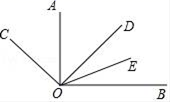A、113° B、134° C、136° D、144°

查看试题解析
10. 定义一种对正整数n的“C运算”：①当n为奇数时，结果为3n+1；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的正整数）并且运算重复进行，例如，n＝66时，其“C运算”如下：

若n＝26，则第2019次“C运算”的结果是（）

A、40 B、5 C、4 D、1

查看试题解析

二、填空题

11. 比较大小：－3－2.1（填“＞”，“＜”或“＝”）．

查看试题解析
12. 如果 $(n - 4) x^{| n - 1 |} y^{2} - 3 x^{2} y - 4 x^{3} + 3$ 是关于 $x$ 、 $y$ 的五次四项式，则 $n =$ 。

查看试题解析
13. 现定义新运算“ $※$ ”，对任意有理数 $a$ 、 $b$ ，规定 $a ※ b = a b + a - b$ ，例如： $1 ※ 2 = 1 \times 2 + 1 - 2 = 1$ ，则计算 $3 ※ (- 5) =$ .

查看试题解析
14. 如果a，b为定值，关于x的一次方程 $\frac{2 k x + a}{3}$ ﹣ $\frac{x - b k}{6}$ ＝2，无论k为何值时，它的解总是1，则a+2b＝．

查看试题解析
15. 如图①，O为直线AB上一点作射线OC，使∠AOC＝120°，将一个直角三角尺如图摆放，直角顶点在点O处，一条直角边OP在射线OA上，将图①中的三角尺绕点O以每秒5°的速度按逆时针方向旋转(如图②所示)，在旋转一周的过程中第t秒时，OQ所在直线恰好平分∠BOC，则t的值为．

查看试题解析

三、解答题

16. 计算：

(1)、 $(- 10) + (+ 3) + (- 5) - (- 7)$

(2)、 ${(- 2)}^{2} \div 4 + (- 3)$

(3)、 ${(- 2)}^{3} \times (\frac{1}{2} - \frac{3}{8}) - | - 2 |$

(4)、 $22^{°} 53^{'} \times 3 + 107^{°} 45^{'} \div 5$

查看试题解析
17. 解下列方程
（Ⅰ）8x＝﹣2（x+4）

（Ⅱ） $\frac{1 - 2 x}{3}$ ＝ $\frac{3 x + 1}{7}$ ﹣3

查看试题解析
18. 先化简，再求值： $5 (3 a^{2} b - a b^{2}) - (a b^{2} + 3 a^{2} b)$ ，其中 $a = \frac{1}{2}$ ， $b = - \frac{1}{3}$

查看试题解析

19. 有20筐白菜，以每筐25千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

与标准质量的差值（千克）	﹣3	﹣2	﹣1.5	0	1	2.5
筐数	1	8	2	3	2	4

(1)、20筐白菜中，最重的一筐比最轻的一筐重多少千克？

(2)、与标准重量比较，20筐白菜总计超过或不足多少千克？

(3)、若白菜每千克售价2.1元，则出售这20筐白菜可卖多少元？

查看试题解析

20. 王老师购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示，根据图中的数据（单位：m），解答下列问题：

(1)、写出用含x、y的整式表示的地面总面积；

(2)、若x=4m，y=1.5m，铺1m²地砖的平均费用为80元，求铺地砖的总费用为多少元？

查看试题解析
21. 已知C为线段AB上一点，关于x的两个方程 $\frac{1}{2}$ （x+1）＝m与 $\frac{2}{3}$ （x+m）＝m的解分别为线段AC ， BC的长，

(1)、当m＝2时，求线段AB的长；

(2)、若C为线段AB的三等分点，求m的值．

查看试题解析
22. 以下是两张不同类型火车的车票：（“D×××次”表示动车，“G×××次”表示高铁）：

(1)、根据车票中的信息填空：两车行驶方向，出发时刻（填“相同”或“不同”）；

(2)、已知该动车和高铁的平均速度分别为200km/h ， 300km/h ，如果两车均按车票信息准时出发，且同时到达终点，求A ， B两地之间的距离；

(3)、在（2）的条件下，请求出在什么时刻两车相距100km？

查看试题解析
23. 如图，已知 $∠ A O B = 60 °$ ， $∠ A O B$ 的边 $O A$ 上有一动点 $P$ ，从距离 $O$ 点 $18 c m$ 的点 $M$ 处出发，沿线段 $M O$ 、射线 $O B$ 运动，速度为 $2 c m / s$ ；动点 $Q$ 从点 $O$ 出发，沿射线 $O B$ 运动，速度为 $1 c m / s$ ； $P$ 、 $Q$ 同时出发，同时射线 $O C$ 绕着点 $O$ 从 $O A$ 上以每秒5°的速度顺时针旋转，设运动时间是 $t (s)$ .

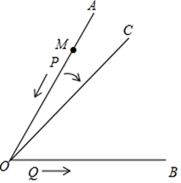(1)、当点 $P$ 在 $M O$ 上运动时， $P O =$ $c m$ （用含 $t$ 的代数式表示）；

(2)、当点 $P$ 在线段 $M O$ 上运动时， $t$ 为何值时， $O P = O Q$ ？此时射线 $O C$ 是 $∠ A O B$ 的角平分线吗？如果是请说明理由.

(3)、在射线 $O B$ 上是否存在 $P$ 、 $Q$ 相距 $2 c m$ ？若存在，请求出t的值并求出此时 $∠ B O C$ 的度数；若不存在，请说明理由.

查看试题解析