河南省邓州市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-12-08 类型:期末考试
一、单选题
-
1. 中国人最早使用负数,可追溯到两千年前的秦汉时期.﹣5的相反数是( )A、±5 B、5 C、 D、﹣2. 下列各式中,正确的是( )A、 B、 C、 D、3. 关于代数式“ ”意义,下列表述错误的是( )A、4个 相乘 B、 的4倍 C、4个 相加 D、4的 倍4. 在等式 中,括号里应填A、 B、 C、 D、5. 某种细菌在培养过程中,每半个小时分裂一次,每次由一个分裂为两个.若这种细菌由 个分裂到 个,这个过程要经过( )A、 小时 B、 小时 C、 小时 D、 小时6. 如图,直线 、 相交于一点, , ,则 ,理由是( )
 A、如果两个角的和等于 ,那么这两个角互余 B、同角(等角)的余角相等 C、如果两个角的和等于 ,那么这两个角互补 D、同角(等角)的补角相等7. 王老师在庆祝中华人民共和国成立70周年的节目中,看到游行的第26号“立德树人”方阵中,“打开的书本”生长出硕果累累的“知识树”,数据链组成的树干上耸立着“教育云”,立刻把如图图形折叠成一个正方体的盒子,折叠后与“育”相对的字是( )
A、如果两个角的和等于 ,那么这两个角互余 B、同角(等角)的余角相等 C、如果两个角的和等于 ,那么这两个角互补 D、同角(等角)的补角相等7. 王老师在庆祝中华人民共和国成立70周年的节目中,看到游行的第26号“立德树人”方阵中,“打开的书本”生长出硕果累累的“知识树”,数据链组成的树干上耸立着“教育云”,立刻把如图图形折叠成一个正方体的盒子,折叠后与“育”相对的字是( )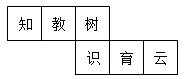 A、知 B、识 C、树 D、教8. 如图,说法正确的是( )
A、知 B、识 C、树 D、教8. 如图,说法正确的是( ) A、 和 是同位角 B、 和 是内错角 C、 和 是同旁内角 D、 和 是同旁内角9. 如图,下列条件中,不能判定 的是( )
A、 和 是同位角 B、 和 是内错角 C、 和 是同旁内角 D、 和 是同旁内角9. 如图,下列条件中,不能判定 的是( ) A、 B、 C、 D、10. 桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )
A、 B、 C、 D、10. 桌上摆放着一个由相同正方体组成的组合体,其俯视图如图所示,图中数字为该位置小正方体的个数,则这个组合体的左视图为( )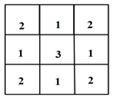 A、
A、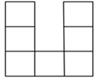 B、
B、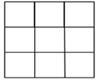 C、
C、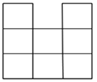 D、
D、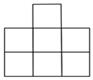
二、填空题
-
11. 比较大小: .(用“ ”或“ ”填空)12. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是 .
 13. 若单项式mx2y与单项式﹣5xny的和是﹣2x2y , 则m+n= .14. 如果y|m|﹣3﹣(m-5)y+16是关于y的二次三项式,则m的值是 .15. 已知,在同一平面内,∠ABC=50°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .
13. 若单项式mx2y与单项式﹣5xny的和是﹣2x2y , 则m+n= .14. 如果y|m|﹣3﹣(m-5)y+16是关于y的二次三项式,则m的值是 .15. 已知,在同一平面内,∠ABC=50°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .三、解答题
-
16. 计算题:(1)、(2)、17.(1)、化简求值: 2(x2y+xy)-3(x2y-xy)-4x2y,其中x=-1,y= .(2)、解答:老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
 +(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式. 18. 数学中,运用整体思想方法在求代数式的值中非常重要.
+(-3x2+5x-7)=-2x2+3x-6.求所捂的多项式. 18. 数学中,运用整体思想方法在求代数式的值中非常重要.例如:已知:a2+2a=1,则代数式2a2+4a+4=2( a2+2a) +4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)、若 ,求 的值;(2)、当 时,代数式 的值是5,求当 时,代数式px3+qx+1的值;(3)、当 时,代数式 的值为m , 求当 时,求代数式 的值是多少?19. 推理与计算:(1)、如图所示,已知线段 ,点 在线段 上, , 是 的中点,那么线段 的长为多少? (2)、如图所示,射线 的方向是北偏东 ,射线 的方向是北偏西 ,若 ,则射线 的方向是北偏东多少度?
(2)、如图所示,射线 的方向是北偏东 ,射线 的方向是北偏西 ,若 ,则射线 的方向是北偏东多少度? 20. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
20. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:碟子的个数
碟子的高度(单位:cm)
1
2
2
2+1.5
3
2+3
4
2+4.5
…
…
 (1)、当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);(2)、分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.21. 已知如图,已知∠1=∠2,∠C=∠D.
(1)、当桌子上放有x(个)碟子时,请写出此时碟子的高度(用含x的式子表示);(2)、分别从三个方向上看,其三视图如上图所示,厨房师傅想把它们整齐叠成一摞,求叠成一摞后的高度.21. 已知如图,已知∠1=∠2,∠C=∠D.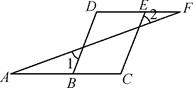 (1)、判断BD与CE是否平行,并说明理由;(2)、说明∠A=∠F的理由.22. 知识链接:
(1)、判断BD与CE是否平行,并说明理由;(2)、说明∠A=∠F的理由.22. 知识链接:“转化、化归思想”是数学学习中常用的一种探究新知、解决问题的基本的数学思想方法,通过“转化、化归”通常可以实现化未知为已知,化复杂为简单,从而使问题得以解决.
(1)、问题背景:已知:△ABC.试说明:∠A+∠B+∠C=180°.问题解决:(填出依据)
解:如图①,延长AB到E,过点B作BF∥AC.

∵BF∥AC(作图)
∴∠1=∠C( )
∠2=∠A( )
∵∠2+∠ABC+∠1=180°(平角的定义)
∴∠A+∠ABC+∠C=180°(等量代换)
小结反思:本题通过添加适当的辅助线,把三角形的三个角之和转化成了一个平角,利用平角的定义,说明了数学上的一个重要结论“三角形的三个内角和等于180°.”
(2)、类比探究:请同学们参考图②,模仿(1)的解决过程试说明“三角形的三个内角和等于180°” (3)、拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E=.
(3)、拓展探究:如图③,是一个五边形,请直接写出五边形ABCDE的五个内角之和∠A+∠B+∠C+∠D+∠E=. 23. 在综合与实践课上,老师请同学们以“两条平行线 , 和一块含 角的直角三角尺 ( , )”为主题开展数学活动.
23. 在综合与实践课上,老师请同学们以“两条平行线 , 和一块含 角的直角三角尺 ( , )”为主题开展数学活动. (1)、如图(1),把三角尺的 角的顶点G放在 上,若 ,求 的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在 和 上,请你探索并说明 与 之间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点F放在 上, 角的顶点E落在 上.若 , ,请用含 , 的式子直接表示 与 的数量关系.
(1)、如图(1),把三角尺的 角的顶点G放在 上,若 ,求 的度数;(2)、如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在 和 上,请你探索并说明 与 之间的数量关系;(3)、如图(3),小亮把三角尺的直角顶点F放在 上, 角的顶点E落在 上.若 , ,请用含 , 的式子直接表示 与 的数量关系.