广西南宁2020-2021学年高一上学期数学期末模拟试卷
试卷更新日期:2020-12-08 类型:期末考试
一、单选题
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、R2. 的值为( )A、 B、 C、 D、3. 已知扇形的圆心角为1,弧长为2,则扇形面积为( )A、1 B、2 C、3 D、44. 若 ,且 ,则 ( )A、 B、 C、 D、5. 已知角 的顶点在坐标原点,始边在 轴非负半轴上,终边与单位圆交于 ,则 ( )A、 B、 C、 D、6. 已知 , ,则 的大小关系为( )A、 B、 C、 D、7. 函数 的零点所在的大致区间是( )A、 B、 C、 D、8. 已知关于 的方程 有两个不等实根,则实数 的取值范围是A、 , B、 C、 , D、9. 若将函数 的图象向左平移 个单位长度后.得到的函数图象关于 对称.则函数 在 上的最小值是( ).A、-1 B、 C、 D、010. 若关于 的不等式 的解集为 ,则 的取值范围是( )A、 B、 C、 D、11. 已知曲线 ,则下面结论正确的是( )A、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线 B、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 C、先将曲线 向左平移 个单位长度,再把所得的曲线上各点横坐标伸长为原来的2倍,纵坐标保持不变,便得到曲线 D、先将曲线 向右平移 个单位长度,再把所得的曲线上各点横坐标缩短为原来的 倍,纵坐标保持不变,便得到曲线12. 已知函数 的部分图象如图所示.则 的解析式为( ).
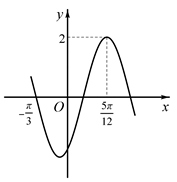 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知正数a,b满足 ,则 的最小值为.14. 已知函数 是定义在 R上的奇函数,且当 时, ,则 的值为 .15. 已知函数 ,若 ,则 的取值范围是.16. 设 ,若关于 的不等式 对任意的 恒成立,则 的最大值为.
三、解答题
-
17. 已知 ,求下列各式的值:(1)、 ;(2)、 .18. 已知集合 ,集合 .(1)、当 时,求 , ;(2)、若 ,求实数m的取值范围.19. 已知函数 的部分图象如图所示,将函数 的图象保持纵坐标不变,横坐标缩短到原来的 ,得到函数 的图象.
 (1)、求函数 的解析式;(2)、求函数 在 上的值域;(3)、求使 成立的 取值的集合.20. 宜城市流水镇是全国闻名的西瓜基地,流水西瓜含糖量高,口感好,多次入选全国农博会并获金奖,畅销全国12省百余个大中城市.实践证明西瓜的产量和品质与施肥关系极大,现研究发现该镇礼品瓜“金皇后”的每亩产量 (单位:百斤)与施用肥料 (单位:百斤)满足如下关系: ,肥料成本投入为 (单位:百元),其它成本投入为 (单位:百元).已知“金皇后”的市场批发价为2元/斤,且销路畅通供不应求,记每亩“金皇后”的利润为 (单位:百元).(1)、求 的函数关系式;(2)、当施用肥料为多少斤时,每亩“金皇后”的利润最大,最大利润是多少元?
(1)、求函数 的解析式;(2)、求函数 在 上的值域;(3)、求使 成立的 取值的集合.20. 宜城市流水镇是全国闻名的西瓜基地,流水西瓜含糖量高,口感好,多次入选全国农博会并获金奖,畅销全国12省百余个大中城市.实践证明西瓜的产量和品质与施肥关系极大,现研究发现该镇礼品瓜“金皇后”的每亩产量 (单位:百斤)与施用肥料 (单位:百斤)满足如下关系: ,肥料成本投入为 (单位:百元),其它成本投入为 (单位:百元).已知“金皇后”的市场批发价为2元/斤,且销路畅通供不应求,记每亩“金皇后”的利润为 (单位:百元).(1)、求 的函数关系式;(2)、当施用肥料为多少斤时,每亩“金皇后”的利润最大,最大利润是多少元?(参考数据: ).