河南省沈丘县槐店回族镇2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-12-07 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、-4是-16的平方根 B、4是(-4)2的平方根 C、(-6)2的平方根是-6 D、 的平方根是±42. 下列计算结果正确的是( ).A、 B、 C、 D、3. 下列从左边到右边的变形,属于因式分解的是( )A、(x+1)(x-1)=x2-1 B、x2-2x+1=x(x-2)+1 C、x2-4y2=(x+4y)(x-4y) D、(x-1)(x-3)+1=(x-2)24. 下列说法:①全等图形的面积相等;②全等图形的周长相等;③面积相等的两三角形全等;④所有正方形都全等.其中正确的结论的个数是( )A、1个 B、2个 C、3个 D、4个5. 如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是根据三角形的全等判定( )
 A、SAS带③ B、SSS带③ C、ASA带③ D、AAS带③6. 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论:①△AOD≌△BOC ②△APC≌△BPD ③PC=PD.其中正确的是( )
A、SAS带③ B、SSS带③ C、ASA带③ D、AAS带③6. 如图所示,在∠AOB的两边截取AO=BO,CO=DO,连结AD、BC交于点P,考察下列结论:①△AOD≌△BOC ②△APC≌△BPD ③PC=PD.其中正确的是( )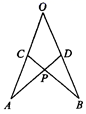 A、①②③ B、只有①② C、只有② D、只有①7. 一个正数的算术平方根是a,那么比这个正数大2的数的算术平方根是( )A、 B、 C、 D、8. 已知△ABC中AD为中线,且AB=5、AC=7 ,则AD的取值范围为( )A、2<AD<12 B、5<AD<7 C、1<AD<6 D、2<AD<109. 一个等腰三角形的两边长分别为4,8,则它的周长为( ).A、12 B、16 C、16或20 D、2010. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于因式分解的恒等式为( )
A、①②③ B、只有①② C、只有② D、只有①7. 一个正数的算术平方根是a,那么比这个正数大2的数的算术平方根是( )A、 B、 C、 D、8. 已知△ABC中AD为中线,且AB=5、AC=7 ,则AD的取值范围为( )A、2<AD<12 B、5<AD<7 C、1<AD<6 D、2<AD<109. 一个等腰三角形的两边长分别为4,8,则它的周长为( ).A、12 B、16 C、16或20 D、2010. 如图,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于因式分解的恒等式为( )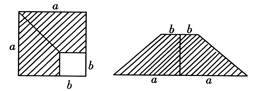 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 设a,b是两个连续的整数,已知 是一个无理数,若 ,是,则 =.12. 若 与 , 则 =13. 如图,点D、E分别在线段AB,AC上,AE=AD,不添加新的线段和字母,要使△ABE≌△ACD,需添加的一个条件是(只写一个条件即可).
 14. 如果 是一个完全平方式,则 的值是.15.
14. 如果 是一个完全平方式,则 的值是.15.大家一定熟知杨辉三角(Ⅰ),观察下列等式(Ⅱ)
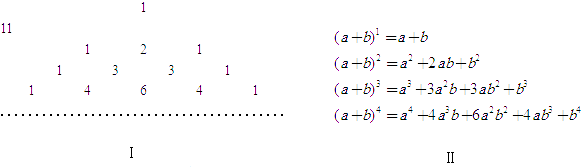
根据前面各式规律,则(a+b)5= .
三、解答题
-
16. 分解因式:(1)、(2)、17. 计算:(1)、(2)、18. 先化简再求值: ,其中x=-219. 如图,点B,E,C,F在一条直线上,AB=DE,AC =DF,BE=CF.求证:△ABC ≌△DEF;
 20. 如果 ,求 的值.21. 如图, 在ΔABC与ΔDCB 中, AC与BD 交于点E,且,∠A=∠D,AB=DC.
20. 如果 ,求 的值.21. 如图, 在ΔABC与ΔDCB 中, AC与BD 交于点E,且,∠A=∠D,AB=DC. (1)、求证:ΔABE≌ΔDCE(2)、当∠AEB=70°时,求∠EBC的度数.22. 如图所示,在四边形ABCD中,CD∥AB,∠ABC的平分线与∠BCD的平分线相交于点F,BF与CD的延长线交于点E,连接CE.
(1)、求证:ΔABE≌ΔDCE(2)、当∠AEB=70°时,求∠EBC的度数.22. 如图所示,在四边形ABCD中,CD∥AB,∠ABC的平分线与∠BCD的平分线相交于点F,BF与CD的延长线交于点E,连接CE.
求证:
(1)、△BCE是等腰三角形.(2)、BC=AB+CD23. 数学课上,老师出示了如下框中的题目:
小敏与同桌小聪讨论后,进行了如下解答:
(1)、特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AEDB(填“>”,“<”或“=”).
 (2)、特例启发,解答题目
(2)、特例启发,解答题目解:题目中,AE与DB的大小关系是:AEDB(填“>”,“<”或“=”)理由如下:如图2,过点E作EF∥BC,交AC于点F,(请你接着继续完成以下解答过程)
(3)、拓展结论,设计新题在等边三角形ABC中,点E在直线上AB上,点D在直线BC上,且ED=EC.若△ABC的边长为3,AE=5,求CD的长(请你直接写出结果).