河北省石家庄市赵县2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-07 类型:期中考试
一、选择题(48分)
-
1. 已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是( )
A、0 B、1 C、2 D、-2 -
2. 若一个正多边形的一个内角是144°,则这个多边形的边数为( )A、12 B、11 C、10 D、9
-
3. 用配方法解下列方程,其中应在两端同时加上4的是( )A、x2-2x=5 B、2x2-4x=5 C、x2+2x= 5 D、x2+4x= 5
-
4. 将y=3x2通过平移,先向上平移2个单位,再向左平移3个单位,可得到抛物线是( )A、y=3(x+3)2-2 B、y=3(x+ 3)2+2 C、y=3(x+2)2-3 D、y= 3(x-2)2+3
-
5. 如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B顺时针旋转到△A'BC'的位置,且点A'、C'仍落在格点上,则线段AB扫过的图形的面积是 平方单位(结果保留π )。( )
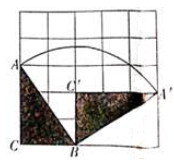 A、 B、 C、 D、
A、 B、 C、 D、 -
6. 一项工程、甲队独做要x天,乙队独做要y天,若甲乙两队合作,所需天数为( )A、 B、 C、 D、x+y
-
7. 在图形的旋转中,下列说法错误的是( )A、图形上的每一点到旋转中心的距离都相等 B、图形上的每一点转动的角度都相同 C、图形上可能存在不动的点 D、旋转前和旋转后的图形全等
-
8. 二次函数y=m2x2-4x+1有最小值-3,则m等于( )A、1 B、-1 C、±1 D、±
-
9. 在同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx的图象可能为( )A、
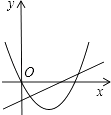 B、
B、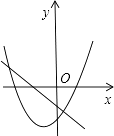 C、
C、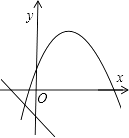 D、
D、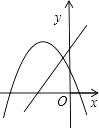
-
10. 若圆锥的底面半径为5cm,侧面积为65πcm2 , 则该圆锥的高是( )A、13cm B、12cm C、11cm D、10cm
-
11. 若m、n是方程x2+x-1=0的两个实数根,则m2+2m+n的值为( )A、0 B、2 C、-1 D、3
-
12. 在平面直角坐标系中,点A的坐标是(3,a),点B的坐标是(b,-1),若点A与点B关于原点O对称,则ab=( )A、3 B、2 C、-6 D、-3
-
13. 如图,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,若∠BAC=25°,则∠P= 度
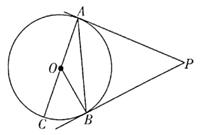 A、30 B、60 C、50 D、75
A、30 B、60 C、50 D、75 -
14. 方程x2-9x+18=0的两个根是等腰三角形的底和腰,则这个等腰三角形的周长为( )A、12 B、15 C、12或15 D、18
-
15. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形
-
16. 要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下( )
甲:若b=5,则点p的个数为0
乙:若b=4,则点P的个数为1
丙:若b=3,则点P的个数为1
A、甲乙错,丙对 B、甲丙对,乙错 C、甲乙对,丙错 D、乙丙对,甲错
二、填空(9分)
-
17. 将方程8x=3x2-1化为一般形式为。
-
18. 九年级(3)班全体同学在圣诞节将自己的贺卡向本班其他同学各赠送一张,全班共互赠了1980张,若全班共有x名学生,则根据题意列出的方程是。
-
19. 观察下列各式数:0,3,8,15,24,……试按此规律写出第n个数是 。
三、解答题(63分)
-
20. 解方程(1)、x2-2x-8= 0(2)、3(x-2)2=x(x-2)
-
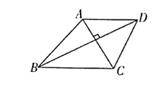
21. 四边形ABCD的两条对角线AC, BD互相垂直,AC+BD=10,当AC,BD的长是多少时,四边形的面积最大?
-
22. 如图,已知△ABC和△A"B"C"及点O。
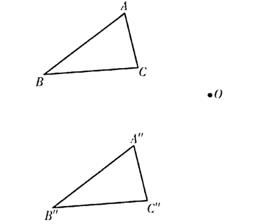
(1)面出△ABC关于点O对称的△A'B'C';
(2)若△A"B"C"与△A'B'C'关于点O'对称,请确定点O'的位。 -
23. AB为⊙O的直径,C是⊙O上的一点,D在AB的延长线上,且∠DCB=∠A,
 (1)、CD与⊙O相切吗?如果相切,请你加以证明;如果不相切,请说明理由。(2)、若∠D=30°,BD=10cm,求⊙O的半径。
(1)、CD与⊙O相切吗?如果相切,请你加以证明;如果不相切,请说明理由。(2)、若∠D=30°,BD=10cm,求⊙O的半径。 -
24. 有一块缺角矩形地皮ABCDE(如下图),其中AB=110m,BC=80m,CD=90m,∠EDC=135°,现准备用此地建一座地基为长方形(图中用阴影部分表示)的数学大楼,建筑公司在接受任务后,设计了A、B、C、D四种方案,请你研究探索应选用哪一种方案,才能使地基面积最大?
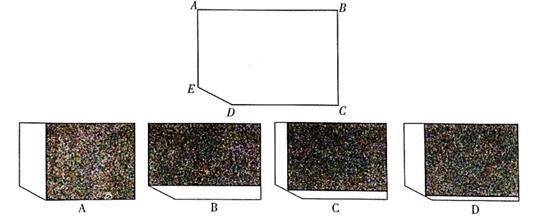 (1)、求出A、B两种方案的面积。(2)、若设地基的面积为S,宽为x,写出方案C(或D)中S与x的关系式。(3)、根据(2)完成下表
(1)、求出A、B两种方案的面积。(2)、若设地基的面积为S,宽为x,写出方案C(或D)中S与x的关系式。(3)、根据(2)完成下表地基的宽x ( m)
50
60
70
75
78
79
80
81
82
地基的面积(m2 )
(4)、根据上表提出你的猜测。(5)、用配方法对(2)中的S与x之间的关系式进行分析,并检验你的猜测是否正确。(6)、你认为A、B、C、D中哪一种方案合理?
