河北省石家庄市赵县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-07 类型:期中考试
一、选择题(本大题有16个小题,共42分。其中1- 10小题各3分,11-16小题各2分。)
-
1. 下列各图形中,具有稳定性的是( )A、
 B、
B、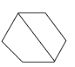 C、
C、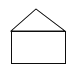 D、
D、 2. 现实世界中,对称现象无处不在,中国的方块字中有的也具有对称性,下列汉字是轴对称图形的是( )A、爱 B、我 C、中 D、华3. 小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm、3cm、8cm、15cm的木条供她选择,那她第三根应选择( )A、2cm B、3cm C、8cm D、15cm4. 如果三角形的一个外角与它不相邻的两个内角的和为 ,那么这个三角形是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、无法确定5. 图中能表示 的BC边上的高的是A、
2. 现实世界中,对称现象无处不在,中国的方块字中有的也具有对称性,下列汉字是轴对称图形的是( )A、爱 B、我 C、中 D、华3. 小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm、3cm、8cm、15cm的木条供她选择,那她第三根应选择( )A、2cm B、3cm C、8cm D、15cm4. 如果三角形的一个外角与它不相邻的两个内角的和为 ,那么这个三角形是( )A、直角三角形 B、钝角三角形 C、锐角三角形 D、无法确定5. 图中能表示 的BC边上的高的是A、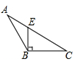 B、
B、 C、
C、 D、
D、 6. 王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )
6. 王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段AD应该是△ABC的( )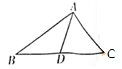 A、角平分线 B、中线 C、高 D、任意一条线7. 如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( )
A、角平分线 B、中线 C、高 D、任意一条线7. 如图,∠A=∠C=90°,AD、BC交于点E,∠2=25°,则∠1的值为( )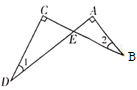 A、55° B、35° C、45° D、25°8. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,点P到边OB的距离为4,则PD=( )
A、55° B、35° C、45° D、25°8. 如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,点P到边OB的距离为4,则PD=( ) A、6 B、5 C、4 D、39. 如图1,已知 ,用尺规作它的角平分线.
A、6 B、5 C、4 D、39. 如图1,已知 ,用尺规作它的角平分线.如图2,步骤如下,
第一步:以B为圆心,以a为半径画弧,分别交射线 BA , BC 于点D,E;
第二步:分别以D,E为圆心,以b为半径画弧,两弧在 内部交于点P;
第三步:画射线 BP .射线 BP 即为所求.
下列正确的是( )
 A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长10. 下列说法正确的是( )A、三角形的中线、角平分线和高都是线段; B、若三条线段的长 、 、 满足 ,则以 、 、 为边一定能组成三角形; C、三角形的外角大于它的任何一个内角; D、三角形的外角和是 .11. 如图,等腰△ABC中,AB=AC= 10,BC=6,直线MN垂直平分AB交AC于D,连接BD,则△BCD的周长等于( )
A、a,b均无限制 B、 , 的长 C、a有最小限制,b无限制 D、 , 的长10. 下列说法正确的是( )A、三角形的中线、角平分线和高都是线段; B、若三条线段的长 、 、 满足 ,则以 、 、 为边一定能组成三角形; C、三角形的外角大于它的任何一个内角; D、三角形的外角和是 .11. 如图,等腰△ABC中,AB=AC= 10,BC=6,直线MN垂直平分AB交AC于D,连接BD,则△BCD的周长等于( ) A、13 B、14 C、15 D、1612. 如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM=2,CN=3,则MN的长为( )
A、13 B、14 C、15 D、1612. 如图,在△ABC中,∠ABC和∠ACB的角平分线交于点E,过点E作MN∥BC交AB于点M,交AC于点N,若BM=2,CN=3,则MN的长为( )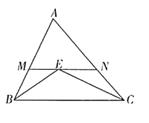 A、10 B、5.5 C、6 D、513. 已知等腰三角形的一个外角等于100°,则它的顶角是( )A、80° 或50° B、20° C、80°或20° D、不能确定14. 在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=∠B=∠C; ④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个15. 如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A、10 B、5.5 C、6 D、513. 已知等腰三角形的一个外角等于100°,则它的顶角是( )A、80° 或50° B、20° C、80°或20° D、不能确定14. 在下列条件中,①∠A+∠B=∠C; ②∠A:∠B:∠C=1:2:3; ③∠A=∠B=∠C; ④∠A=∠B=2∠C; ⑤∠A=2∠B=3∠C,能确定△ABC为直角三角形的条件有( )A、2个 B、3个 C、4个 D、5个15. 如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )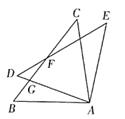 A、15° B、20° C、25° D、30°16. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有( )
A、15° B、20° C、25° D、30°16. 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论要:①AE= BD;②AG= BF ;③FG∥BE;④OC平分∠BOE,其中结论正确的个数有( )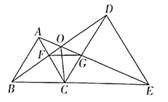 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(本大题有3个小题,共12分,17-18小题各3分;19小题有3个空,每空2分)
-
17. 如图,已知∠1=∠2,请你添加一个条件 , 使得△ABD≌△ACD。(添一个即可)
 18. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△ABC等于。
18. 如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,若S△DEF=2,则S△ABC等于。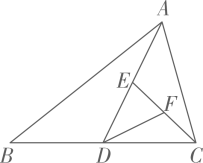 19. 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A= , ∠A3= , 若∠A=α,则∠A2018为。
19. 如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A=64°,则∠A= , ∠A3= , 若∠A=α,则∠A2018为。
三、解答题(本大题有7个小题,共66分)
-
20. 已知n边形的内角和θ=(n-2)×180°(1)、当θ=900°时,求出边数n;(2)、小明说θ能取800°,这种说法对吗?若对,求出边数n;若不对,说明理由。21. 已知a,b,c是△ABC的三边长。(1)、若a,b,c满足|a-b|+|b-c|=0,试判断△ABC的形状。(2)、若a,b,c满足(a-b)(b-c)=0,试判断△ABC的形状。22. 琪琪家门前有一条小河,村里准备在河面上架上一座桥,但河宽AB无法直接测量,(1)、爱动脑的小明想到了如下方法:在与AB垂直的岸边BF上取两点C,D,使CD= , 再引出BF的垂线DG,在DG上取一点E,并使A、C、E在一条直线上,这时测出线段的长度就是AB的长。

按小明的想法填写题目中的空格;
(2)、请完成推理过程。23. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=50°,求∠DAC及∠BOA的度数。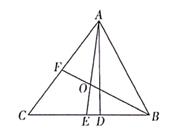 24. 如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3) ,B(1,0),C(1,2)。
24. 如图,在平面直角坐标系xOy中,△ABC的三个顶点的坐标分别是A(2,3) ,B(1,0),C(1,2)。 (1)、在图中画出△ABC关于y轴对称的△A1B1C1(2)、直接写出A1 , B1 , C1三点的坐标:A1( ),B1( ),C1( );(3)、如果要使以B、C、D为顶点的三角形与△ABC全等,直接写出所有符合条件的点D坐标。25. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。
(1)、在图中画出△ABC关于y轴对称的△A1B1C1(2)、直接写出A1 , B1 , C1三点的坐标:A1( ),B1( ),C1( );(3)、如果要使以B、C、D为顶点的三角形与△ABC全等,直接写出所有符合条件的点D坐标。25. 已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B都在直线l的同侧),AD⊥l,BE⊥l,亚足分别为D、E。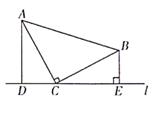 (1)、求证:△ADC≌△CEB.(2)、请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。26. 在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。
(1)、求证:△ADC≌△CEB.(2)、请判断DE、BE、AD三条线段之间有怎样的数基关系,并证明。26. 在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE。 (1)、如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=。(2)、设∠BAC=α,∠BCE=β
(1)、如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=。(2)、设∠BAC=α,∠BCE=β①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由。
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论。