山东省潍坊市临朐县、诸城市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 下面的图形中对称轴最多的是( )A、
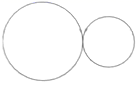 B、
B、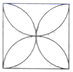 C、
C、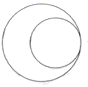 D、
D、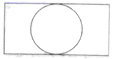 2. 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
2. 如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )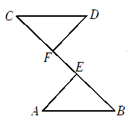 A、AE=DF B、∠A=∠D C、∠B=∠C D、AB= CD3. 下列各式中,无论 取何值分式都有意义的是( )A、 B、 C、 D、4. 如图,直线 , , ,则 的度数是( )
A、AE=DF B、∠A=∠D C、∠B=∠C D、AB= CD3. 下列各式中,无论 取何值分式都有意义的是( )A、 B、 C、 D、4. 如图,直线 , , ,则 的度数是( )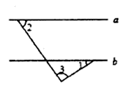 A、 B、 C、 D、5. 下列语句是命题的是( )
A、 B、 C、 D、5. 下列语句是命题的是( )⑴两点之间,线段最短.(2)如果 ,那么 吗?(3)如果两个角的和是90度,那么这两个角互余.(4)过直线外一点作已知直线的垂线.
A、(1)(2) B、(3)(4) C、(1)(3) D、(2)(4)6. 已知 △ABC(如图1),按图2图3所示的尺规作图痕迹,(不需借助三角形全等)就能推出四边形ABCD是平行四边形的依据是( )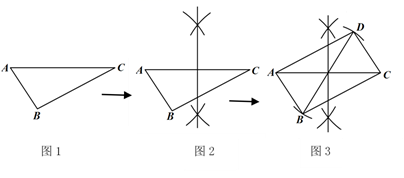 A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形7. 某中学篮球队12名队员的年龄情况如下:
A、两组对边分别平行的四边形是平行四边形 B、对角线互相平分的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、两组对边分别相等的四边形是平行四边形7. 某中学篮球队12名队员的年龄情况如下:年龄(单位:岁)
14
15
16
17
18
人数
1
5
3
2
1
则这个队队员年龄的众数和中位数分别是( )
A、15,16 B、15,15 C、15,15.5 D、16,158. 若解关于 的方程 时产生增根,那么 的值为( )A、1 B、2 C、0 D、-19. 如图,在正方形 内,以 为边作等边三角形 ,连接 并延长交 于 ,则下列结论错误的是( )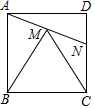 A、 B、 C、 D、10. 如图,在 中,点 为 的中点, 为 的外角平分线,且 ,若 ,则 的长为( )
A、 B、 C、 D、10. 如图,在 中,点 为 的中点, 为 的外角平分线,且 ,若 ,则 的长为( ) A、3 B、 C、5 D、11. 如图, ▱ ABCD的对角线 、 交于点 ,顺次联结 ▱ ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:① ⊥ ;② ;③ ;④ ,可以使这个新的四边形成为矩形,那么这样的条件个数是( )
A、3 B、 C、5 D、11. 如图, ▱ ABCD的对角线 、 交于点 ,顺次联结 ▱ ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:① ⊥ ;② ;③ ;④ ,可以使这个新的四边形成为矩形,那么这样的条件个数是( )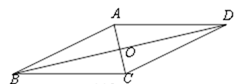 A、1个; B、2个; C、3个; D、4个.12. 如图,△ABC中,AD垂直BC于点D , 且AD=BC , BC上方有一动点P满足 ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
A、1个; B、2个; C、3个; D、4个.12. 如图,△ABC中,AD垂直BC于点D , 且AD=BC , BC上方有一动点P满足 ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )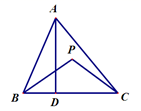 A、30° B、45° C、60° D、90°
A、30° B、45° C、60° D、90°二、填空题
-
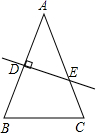
13. 如图,在 中, 是 的垂直平分线,且分别交 于点 和 , ,则 等于度.
 14. 数学老师计算同学们一学期的平均成绩时,将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、100分、90分,则小红一学期的数学平均成绩是分.15. 如图,延长矩形 的边 至点 ,使 .连接 ,如果 ,则 等于度.
14. 数学老师计算同学们一学期的平均成绩时,将平时、期中和期末的成绩按3:3:4计算,若小红平时、期中和期末的成绩分别是90分、100分、90分,则小红一学期的数学平均成绩是分.15. 如图,延长矩形 的边 至点 ,使 .连接 ,如果 ,则 等于度.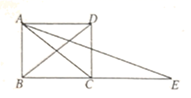 16. 小明用S2= [(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .17. 如图(1)是长方形纸带, ,将纸带沿 折叠图(2)形状,则 等于度.
16. 小明用S2= [(x1﹣3)2+(x2﹣3)2+…+(x10﹣3)2]计算一组数据的方差,那么x1+x2+x3+…+x10= .17. 如图(1)是长方形纸带, ,将纸带沿 折叠图(2)形状,则 等于度.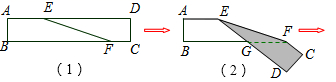 18. 如图,在四边形 中, 是 的中点.点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒3个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动,当运动时间为 秒时,以点 为顶点的四边形是平行四边形,则 的值等于 .
18. 如图,在四边形 中, 是 的中点.点 以每秒1个单位长度的速度从点 出发,沿 向点 运动;点 同时以每秒3个单位长度的速度从点 出发,沿 向点 运动.点 停止运动时,点 也随之停止运动,当运动时间为 秒时,以点 为顶点的四边形是平行四边形,则 的值等于 .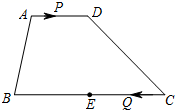
三、解答题
-
19. 计算:(1)、(2)、(3)、20. 阅读材料,并回答问题:
在一个含有多个字母的式子中,若任意交换两个字母的位置,式子的值不变,则这样的式子叫做对称式.例如: 等都是对称式.
(1)、在下列式子中,属于对称式的序号是;① ②a-b ③ ④ .
(2)、若 ,用 表示 ,并判断 的表达式是否为对称式;当 时,求对称式 的值.21. 某市举行知识大赛, 校、 校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.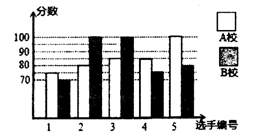 (1)、根据图示填写下表:
(1)、根据图示填写下表:平均数
中位数
众数
校选手成绩
85
校选手成绩
85
80
(2)、结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;(3)、计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.22. 如图,平行四边形 的对角线 交于点 ,分别过点 作 ,连接 交 于点 .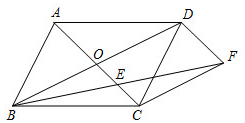 (1)、求证: ;(2)、当 等于多少度时,四边形 为菱形?请说明理由.23. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?24. 如图所示,四边形 是正方形, 是 延长线上一点.直角三角尺的一条直角边经过点 ,且直角顶点 在 边上滑动(点 不与点 重合),另一直角边与 的平分线 相交于点 .
(1)、求证: ;(2)、当 等于多少度时,四边形 为菱形?请说明理由.23. 某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?24. 如图所示,四边形 是正方形, 是 延长线上一点.直角三角尺的一条直角边经过点 ,且直角顶点 在 边上滑动(点 不与点 重合),另一直角边与 的平分线 相交于点 .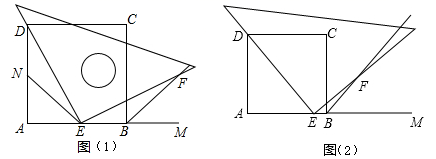 (1)、求证: ;(2)、如图(1),当点 在 边的中点位置时,猜想 与 的数量关系,并证明你的猜想;(3)、如图(2),当点 在 边(除两端点)上的任意位置时,猜想此时 与 有怎样的数量关系,并证明你的猜想.
(1)、求证: ;(2)、如图(1),当点 在 边的中点位置时,猜想 与 的数量关系,并证明你的猜想;(3)、如图(2),当点 在 边(除两端点)上的任意位置时,猜想此时 与 有怎样的数量关系,并证明你的猜想.