山东省潍坊市安丘市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点 $M (3 ， - 2)$ 与点 $N$ 关于 $x$ 轴对称，则点 $N$ 的坐标是（）

A、 $(- 3 ， - 2)$ B、 $(- 3 ， 2)$ C、 $(3 ， 2)$ D、 $(2 ， - 3)$

查看试题解析
2. 如图，线段 $A D$ 与 $B C$ 交于点 $O$ ，且 $A C = B D ， A D = B C$ ，则下面的结论中错误的是（）

A、 $Δ A B C ≅ Δ B A D$ B、 $O B = O C$ C、 $∠ C A B = ∠ D B A$ D、 $∠ C = ∠ D$

查看试题解析
3. 在△ABC中，AB=AC，∠A=80°，进行如下操作：
①以点B为圆心，以小于AB长为半径作弧，分别交BA、BC于点E、F；
②分别以E、F为圆心，以大于 $\frac{1}{2}$ EF长为半径作弧，两弧交于点M；
③作射线BM交AC于点D，
则∠BDC的度数为（）

A、100° B、65° C、75° D、105°

查看试题解析
4. 使分式 $\frac{x}{2 x- 4}$ 有意义的x的取值范围是（）

A、x=2 B、x≠2且x≠0 C、x=0 D、x≠2

查看试题解析
5. 某画室分两次购买了相同的素描本，第一次用120元购买了若干本，第二次在同一家商店又购买了240元，这次商家每本优惠4元，结果比上次多买了20本.设第一次买了x本素描本，列方程正确的是（）

A、 $\frac{120}{x} - \frac{240}{x + 20} = 4$ B、 $\frac{240}{x + 20} - \frac{120}{x} = 4$ C、 $\frac{120}{x} - \frac{240}{x - 20} = 4$ D、 $\frac{240}{x - 20} - \frac{120}{x} = 4$

查看试题解析
6. 下列关于分式方程增根的说法正确的是（）

A、使所有的分母的值都为零的解是增根 B、分式方程的解为零就是增根 C、使分子的值为零的解就是增根 D、使最简公分母的值为零的解是增根

查看试题解析
7. 在一次数学测验中，甲、乙、丙、丁四位同学的分数分别是90、x、90、70，若这四个同学得分的众数与平均数恰好相等，则他们得分的中位数是（）

A、100 B、90 C、80 D、70

查看试题解析
8. 甲、乙、丙、丁四名设计运动员参加射击预选赛，他们射击成绩的平均数及方差如下表示：若要选出一个成绩较好状态稳定的运动员去参赛，那么应选运动员（）

甲

乙

丙

丁

$\bar{x}$

8

9

9

8

$s^{2}$

1.2

1

1.2

1

A、甲 B、乙 C、丙 D、丁

查看试题解析
9. 下列命题中，是真命题的是（）
①两条直线被第三条直线所截，同位角相等；
②在同一平面内，垂直于同一直线的两条直线互相平行
③三角形的三条高中，必有一条在三角形的内部
④三角形的三个外角一定都是锐角

A、①② B、②③ C、①③ D、③④

查看试题解析
10. 如图，点A，B为定点，定直线l//AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：
①线段MN的长；

②△PAB的周长；

③△PMN的面积；

④直线MN，AB之间的距离；

⑤∠APB的大小．

其中会随点P的移动而变化的是（）

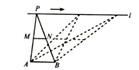A、②③ B、②⑤ C、①③④ D、④⑤

查看试题解析
11. 小明用两根同样长的竹棒做对角线，制作四边形的风筝，则该风筝的形状一定是（　）

A、矩形 B、正方形 C、等腰梯形 D、无法确定

查看试题解析
12. 如图，正方形ABCD中，E，F分别为AB，CD的中点，连接DE，BF，CE，AF，正方形ABCD的面积为1，则阴影部分的面积为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析

二、填空题

13. 如果△ABC的三边长分别为7，5，3，△DEF的三边长分别为2x﹣1，3x﹣2，3，若这两个三角形全等，则x= ．

查看试题解析
14. 已知 $\frac{a - b}{a} = \frac{1}{5}$ ，则 $\frac{a}{a + b} =$ ．

查看试题解析
15. 计算： ${(\frac{a b^{2}}{c})}^{2} \cdot {(- \frac{c^{2}}{a b})}^{3} \div {(\frac{b c}{a})}^{2} =$ ．

查看试题解析
16. 某单位定期对员工按照专业能力、工作业绩、考勤情况三方面进行考核（每项满分100分），三者权重之比为 $3 ： 5 ： 2$ ，小明经过考核后三项分数分别为90分，86分，83分，则小明的最后得分为分．

查看试题解析
17. 如图，已知△ABC中， ∠ABC的平分线与∠ACE的平分线交于点D，若∠A=50°，则∠D=度．

查看试题解析
18. 用“如果…，那么…”的形式，写出“对顶角相等”的逆命题：.

查看试题解析
19. 如图，在正方形 $A B C D$ 的内侧，作等边 $Δ D C E$ ，则 $∠ B A E$ 的度数是．

查看试题解析
20. 如图， $C$ 在直线 $B E$ 上， $∠ A = m ° ， ∠ A B C$ 与 $∠ A C E$ 的角平分线交于点 $A_{1}$ ，则 $A_{1} =$ $°$ ；若再作 $∠ A_{1} B E 、 ∠ A_{1} C E$ 的平分线，交于点 $A_{2}$ ；再作 $∠ A_{2} B E 、 ∠ A_{2} C E$ 的平分线，交于点 $A_{3}$ ；依此类推， $∠ A_{10} =$ $°$ ．

查看试题解析

三、解答题

21.

(1)、先化简，再求值： $(a + 1 - \frac{4 a - 5}{a - 1}) \div (\frac{1}{a - 1} - \frac{2}{a^{2} - a})$ ，其中 $a = 4$

(2)、解分式方程： $\frac{8}{y^{2} - 4} + 1 = \frac{y}{y - 2}$

查看试题解析
22. 如图，在矩形 $A B C D$ 中， $D E ⊥ A C ， B F ⊥ A C$ ，垂足分别为 $E ， F ， D E = B F$ ，连接 $D F ， B E$ ．
求证：四边形 $D E B F$ 是平行四边形．

查看试题解析
23. 某公司购买了一批A、B型芯片，其中A型芯片的单价比B型芯片的单价少9元，已知该公司用3120元购买A型芯片的条数与用4200元购买B型芯片的条数相等．

(1)、求该公司购买的A、B型芯片的单价各是多少元？

(2)、若两种芯片共购买了200条，且购买的总费用为6280元，求购买了多少条A型芯片？

查看试题解析
24. 如图，由6个长为2，宽为1的小矩形组成的大矩形网格，小矩形的顶点称为这个矩形网格的格点，由格点构成的几何图形称为格点图形（如：连接2个格点，得到一条格点线段；连接3个格点，得到一个格点三角形；…），请按要求作图（标出所画图形的顶点字母）．

(1)、画出4种不同于示例的平行格点线段；

(2)、画出4种不同的成轴对称的格点三角形，并标出其对称轴所在线段；

(3)、画出1个格点正方形，并简要证明．

查看试题解析
25. 如图，在 $R t Δ A B C$ 中， $∠ B = 90^{°} ， A C = 2 A B$ ．将 $A B$ 向上翻折，使点 $B$ 落在 $A C$ 上，记为点 $E$ ，折痕为 $A D$ ，再将 $Δ A D E$ 以 $A C$ 为对称轴翻折至 $Δ A E F$ ，连接 $F C$ ．

(1)、证明： $A D = C D$

(2)、猜想四边形 $A D C F$ 的形状并证明．

查看试题解析
26. 如图，在等边 $Δ A B C$ 中， $D ， E$ 分别为 $A B ， A C$ 的中点，延长 $B C$ 至点 $F$ ，使 $C F = \frac{1}{2} B C$ ，连结 $C D$ 和 $E F$ ．

(1)、求证： $C D = E F$

(2)、猜想： $Δ A B C$ 的面积与四边形 $B D E F$ 的面积的关系，并说明理由．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	8	9	9	8
$s^{2}$	1.2	1	1.2	1