山东省泰安市新泰市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 在实数 (相邻两个2中间一次多1个0)中,无理数有( )A、2个 B、3个 C、4个 D、5个2. 的平方根是( )A、±5 B、5 C、± D、3. 电话卡上存有4元话费,通话时每分钟话费 元,则电话卡上的余额 (元)与通话时间 (分钟)之间的函数图象是图中的( )A、
 B、
B、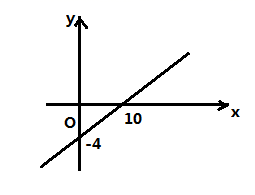 C、
C、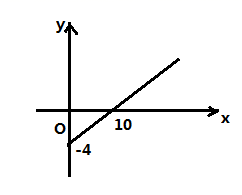 D、
D、 4. 下列图案中,是轴对称图形的有( )个.
4. 下列图案中,是轴对称图形的有( )个. A、1 B、2 C、3 D、45. 一次函数y=ax+b与y=abx在同一个平面直角坐标系中的图象不可能是( )A、
A、1 B、2 C、3 D、45. 一次函数y=ax+b与y=abx在同一个平面直角坐标系中的图象不可能是( )A、 B、
B、 C、
C、 D、
D、 6. 周长38 的三角形纸片 (如图甲), ,将纸片按图中方式折叠,使点 与点 重合,折痕为 (如图乙),若 的周长为25 ,则 的长为( )
6. 周长38 的三角形纸片 (如图甲), ,将纸片按图中方式折叠,使点 与点 重合,折痕为 (如图乙),若 的周长为25 ,则 的长为( ) A、10 B、12 C、15 D、137. 如图,已知 为 的中点,若 ,则 ( )
A、10 B、12 C、15 D、137. 如图,已知 为 的中点,若 ,则 ( ) A、5 B、6 C、7 D、8. 对于一次函数 ,下列说法正确的是( )A、它的图象经过点 B、它的图象与直线 平行 C、 随 的增大而增大 D、当 时, 随 的增大而减小9. 象棋在中国有三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,若表示棋子“馬”和“車”的点的坐标分别为 ,则表示棋子“炮”的点的坐标为( )
A、5 B、6 C、7 D、8. 对于一次函数 ,下列说法正确的是( )A、它的图象经过点 B、它的图象与直线 平行 C、 随 的增大而增大 D、当 时, 随 的增大而减小9. 象棋在中国有三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏,如图,若表示棋子“馬”和“車”的点的坐标分别为 ,则表示棋子“炮”的点的坐标为( ) A、 B、 C、 D、10. 如图, 中, 与 的平分线交于点 ,过点 作 交 于点 ,交 于点 ,那么下列结论:
A、 B、 C、 D、10. 如图, 中, 与 的平分线交于点 ,过点 作 交 于点 ,交 于点 ,那么下列结论:① 是等腰三角形;② ;③若 , ;④ .其中正确的有( )
 A、4个 B、3个 C、2个 D、1个11. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛的路程y(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的有( )
A、4个 B、3个 C、2个 D、1个11. 甲、乙两队举行了一年一度的赛龙舟比赛,两队在比赛的路程y(米)与时间t(分钟)之间的函数关系如图所示,请你根据图象判断,下列说法正确的有( )①甲队先到达终点;
②甲队比乙队多走200米路程;
③乙队比甲队少用0.2分钟;
④比赛中两队从出发到2.2分钟时间段,乙队的速度比甲队的速度快.
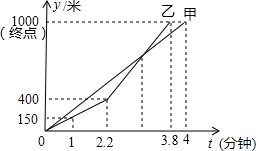 A、1个 B、2个 C、3个 D、4个12. 如图,高速公路上有 两点相距10km,为两村庄,已知 于 , 于 ,现要在 上建一个服务站 ,使得 两村庄到 站的距离相等,则 的长是( )km.
A、1个 B、2个 C、3个 D、4个12. 如图,高速公路上有 两点相距10km,为两村庄,已知 于 , 于 ,现要在 上建一个服务站 ,使得 两村庄到 站的距离相等,则 的长是( )km. A、4 B、5 C、6 D、
A、4 B、5 C、6 D、二、填空题
-
13. 若一个正数的平方根是2a﹣1和﹣a+2,则这个正数是 .14. 如图,在三角形纸片 中, ,折叠纸片,使点 落在 边上的点 处,折痕 与 交于点 ,则折痕 的长为;
 15. 如图,小明站在离水面高度为8米的岸上点 处用绳子拉船靠岸,开始时绳子 的长为17米,小明以1米每秒的速度收绳,7秒后船移动到点 的位置,问船向岸边移动了米( 的长)(假设绳子是直的).
15. 如图,小明站在离水面高度为8米的岸上点 处用绳子拉船靠岸,开始时绳子 的长为17米,小明以1米每秒的速度收绳,7秒后船移动到点 的位置,问船向岸边移动了米( 的长)(假设绳子是直的). 16. 表中给出了直线 上部分点 的坐标值.
16. 表中给出了直线 上部分点 的坐标值.-2
0
2
4
3
1
-1
-3
则直线 与两坐标轴围成的三角形面积等于 .
17. 若 与点 关于 轴对称,则 的值是;18. 如图, ,则 .
三、解答题
-
19. 阅读下面的文字,解答问题,例如: ,即 ,
的整数部分是2,小数部分是 ;
(1)、试解答: 的整数部分是 , 小数部分是(2)、已知 小数部分是 , 小数部分是 ,且 ,请求出满足条件的 的值.20. 如图, 三个顶点坐标分别是 (1)、请画出 关于 轴对称的 ;(2)、直接写出 的坐标;(3)、求出 的面积.21. 某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为 元、 元.(1)、根据题意,填写下表:
(1)、请画出 关于 轴对称的 ;(2)、直接写出 的坐标;(3)、求出 的面积.21. 某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为 元、 元.(1)、根据题意,填写下表:老年人数量(人)
5
10
20
甲旅行社收费(元)
300
乙旅行社收费)(元)
800
(2)、求 、 关于x的函数关系式(不用写出自变量的取值范围)?(3)、如果 ,选择哪家旅行社合算?22. 如图,△ABC中,AB=AC,D是AC边上的一点,CD=1,BC= ,BD=2. (1)、求证:ΔBCD是直角三角形;(2)、求△ABC的面积。23. 阅读解答题:
(1)、求证:ΔBCD是直角三角形;(2)、求△ABC的面积。23. 阅读解答题:(几何概型)
条件:如图1: 是直线 同旁的两个定点.
问题:在直线 上确定一点 ,使 的值最小;
方法:作点 关于直线 对称点 ,连接 交 于点 ,则 ,
由“两点之间,线段最短”可知,点 即为所求的点.
 (1)、(模型应用)
(1)、(模型应用)如图2所示:两村 在一条河 的同侧, 两村到河边 的距离分别是 千米, 千米, 千米,现要在河边 上建造一水厂,向 两村送水,铺设水管的工程费用为每千米20000元,请你在 上选择水厂位置,使铺设水管的费用最省,并求出最省的铺设水管的费用 .
(2)、(拓展延伸)如图, 中,点 在边 上,过 作 交 于点 , 为 上一个动点,连接 ,若 最小,则点 应该满足( )(唯一选项符合题意)
 A、 B、 C、 D、
A、 B、 C、 D、

