山东省泰安市岱岳区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 下列因式分解结果正确的是( )A、2a2﹣4a=a(2a﹣4) B、 C、2x3y﹣3x2y2+x2y=x2y(2x﹣3y) D、x2+y2=(x+y)22. 如图汽车标志中不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若分式 的值为0,则( )A、 B、 C、 D、4. 下列能作为多边形内角和的是( )A、 B、 C、 D、5. 以下是某校九年级10名同学参加学校演讲比赛的统计表:
3. 若分式 的值为0,则( )A、 B、 C、 D、4. 下列能作为多边形内角和的是( )A、 B、 C、 D、5. 以下是某校九年级10名同学参加学校演讲比赛的统计表:成绩/分
80
85
90
95
人数/人
1
2
5
2
则这组数据的中位数和平均数分别为( )
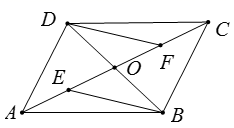
A、90,90 B、90,89 C、85,89 D、85,906. 若六边形的最大内角为m度,则必有( )A、 B、 C、 D、7. ▱ABCD中,E,F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A、BE=DF B、AE=CF C、AF//CE D、∠BAE=∠DCF8. 如图,在平面直角坐标系中,将 绕 点逆时针旋转 后, 点对应点的坐标为( ) A、 B、 C、 D、9. 如图,在 中, ,将 在平面内绕点 旋转到 的位置,使 ,则旋转角的度数为( )
A、 B、 C、 D、9. 如图,在 中, ,将 在平面内绕点 旋转到 的位置,使 ,则旋转角的度数为( ) A、 B、 C、 D、10. 如图,在▱ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A、 B、 C、 D、10. 如图,在▱ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )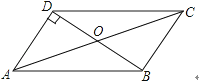 A、4cm B、5cm C、6cm D、8cm11. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
A、4cm B、5cm C、6cm D、8cm11. 如图,▱ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )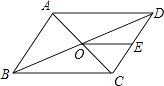 A、15 B、18 C、21 D、2412. 如图,在 中,点 为 的中点, 平分 ,且 于点 ,延长 交 于点 .若 , ,则 的长为( )
A、15 B、18 C、21 D、2412. 如图,在 中,点 为 的中点, 平分 ,且 于点 ,延长 交 于点 .若 , ,则 的长为( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题
-
13. 当 取时,分式 无意义;14. 若a-b=1,则 的值为 .15. 若关于x的分式方程 有增根,则m的值为.16. 如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.
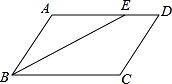 17. 如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于
17. 如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于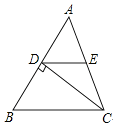 18. 如图1六边形的内角和 为 度,如图2六边形的内角和 为 度,则m-n= .
18. 如图1六边形的内角和 为 度,如图2六边形的内角和 为 度,则m-n= .
三、解答题
-
19. 先化简,再求值: ,其中 .20. 2013年6月,某中学结合广西中小学阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
 (1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;(4)、如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.21. 为改善生态环境,防止水土流失,某村计划在荒坡上种1000棵树.由于青年志愿者的支援,每天比原计划多种25%,结果提前5天完成任务,原计划每天种多少棵树?22. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.
(1)、在这次抽样调查中,一共调查了多少名学生?(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;(4)、如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数.21. 为改善生态环境,防止水土流失,某村计划在荒坡上种1000棵树.由于青年志愿者的支援,每天比原计划多种25%,结果提前5天完成任务,原计划每天种多少棵树?22. 如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF.