山东省日照市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如下图,线段 是 的高的是( )A、
2. 如下图,线段 是 的高的是( )A、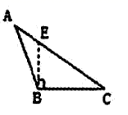 B、
B、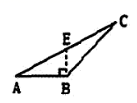 C、
C、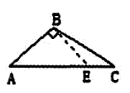 D、
D、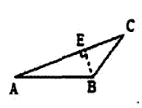 3. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )
3. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )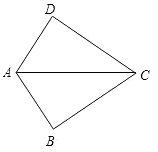 A、 B、 C、 D、4. 下列计算中正确的是( ).A、 B、 C、 D、5. 下列各式是完全平方式的是( )A、 B、 C、x+xy+1 D、6. 若分式 的值为正数,则x的取值范围是( )A、 B、 C、 D、 且7. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A、 B、 C、 D、4. 下列计算中正确的是( ).A、 B、 C、 D、5. 下列各式是完全平方式的是( )A、 B、 C、x+xy+1 D、6. 若分式 的值为正数,则x的取值范围是( )A、 B、 C、 D、 且7. 如图,△ABC的面积为1cm2 , AP垂直∠B的平分线BP于P,则△PBC的面积为( ) A、0.4 cm2 B、0.5 cm2 C、0.6 cm2 D、0.7 cm28. 如图,ΔABC≌ΔADE,AB=AD, AC=AE,∠B=28°,∠E=95°,∠EAB=20°,则∠BAD为( )
A、0.4 cm2 B、0.5 cm2 C、0.6 cm2 D、0.7 cm28. 如图,ΔABC≌ΔADE,AB=AD, AC=AE,∠B=28°,∠E=95°,∠EAB=20°,则∠BAD为( )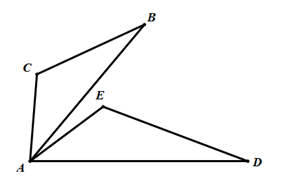 A、77° B、57° C、55° D、75°9. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )
A、77° B、57° C、55° D、75°9. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是( )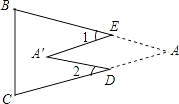 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 若关于 的方程 有正数根,则k的取值范围是( )A、 B、 C、 D、 且11. 已知:如图,四边形 中, , .在 边上求作点 ,则 的最小值为( )
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)10. 若关于 的方程 有正数根,则k的取值范围是( )A、 B、 C、 D、 且11. 已知:如图,四边形 中, , .在 边上求作点 ,则 的最小值为( ) A、4 B、6 C、8 D、1012. 如图,已知 ,点 ...在射线 上,点 ...在射线 上; ...均为等边三角形,若 ,则 的边长为( )
A、4 B、6 C、8 D、1012. 如图,已知 ,点 ...在射线 上,点 ...在射线 上; ...均为等边三角形,若 ,则 的边长为( )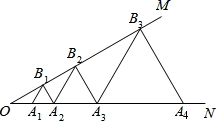 A、4038 B、4010 C、 D、
A、4038 B、4010 C、 D、二、填空题
-
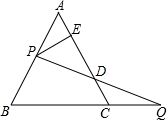
13. 已知等腰三角形的一个内角是 ,则它的底角是 .14. 当x=1时,分式 无意义;当x=2时,分式 的值为0,则a+b= .15. 若 是关于x的完全平方式,则m= .16. 若5x-3y-2=0,则105x÷103y=。17. 如图,边长为 的等边 中,一动点 沿 从 向 移动,动点 以同样的速度从 出发沿 的延长线运动,连 交 边于 ,作 于 ,则 的长为 .
三、解答题
-
18. 先化简,再求值:(4ab3-8a2b2)÷4ab+(2a+b)(2a-b),其中a=2,b=1.19.(1)、解方程:(2)、先化简后求值 ,其中 满足20. 已知:从 边形的一个顶点出发共有4条对角线;从 边形的一个顶点出发的所有对角线把 边形分成6个三角形;正 边形的边长为 ,周长为63.求 的值.21. 某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.(1)、这项工程的规定时间是多少天?(2)、已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?22. 图①是一个长为 、宽为 的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
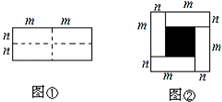 (1)、请用两种不同的方法求图②中阴影部分的面积.
(1)、请用两种不同的方法求图②中阴影部分的面积.方法1:;
方法2:;
(2)、观察图②请你写出下列三个代数式: 之间的等量关系.(3)、根据(2)题中的等量关系,解决如下问题:①已知: ,求 的值;
②已知: ,求: 的值.
23. 阅读
(1)、阅读理解: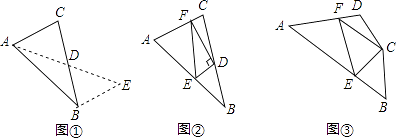
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.
中线AD的取值范围是;
(2)、问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)、问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.