山东省青岛市莱西市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 使分式 $\frac{3 x}{x + 2}$ 有意义的x的取值范围为（）

A、x≠﹣2 B、x≠2 C、x≠0 D、x≠±2

查看试题解析
2. 下列多项式中能用完全平方公式分解的是（）

A、x²﹣x+1 B、1﹣2x+x² C、﹣a²+b²﹣2ab D、4x²+4x﹣1

查看试题解析
3. 如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF ，则四边形ABFD的周长是（）

A、8 B、10 C、12 D、14

查看试题解析
4. 关于x的方程 $\frac{3 x - 2}{x + 1} = 2 + \frac{m}{x + 1}$ 无解，则m的值为（）

A、﹣5 B、﹣8 C、﹣2 D、5

查看试题解析
5. 二班学生某次测试成绩统计如下表：则得分的众数和中位数分别是（）

得分（分）

60

70

80

90

100

人数（人）

7

12

10

8

3

A、70分，70分 B、80分，80分 C、70分，80分 D、80分，70分

查看试题解析
6. 如图，在边长为4的正方形ABCD中，E是AB边上的一点，且AE=3，Q为对角线AC上的动点，则△BEQ周长的最小值为（）

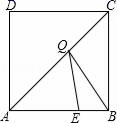A、5 B、6 C、 $4 \sqrt{2}$ D、8

查看试题解析
7. 如图，在△ABC 中，点 D 是边 BC 上的点（与 B、C 两点不重合），过点 D作 DE∥AC ， DF∥AB ，分别交 AB、AC 于 E、F 两点，下列说法正确的是（）

A、若 AD 平分∠BAC ，则四边形 AEDF 是菱形 B、若 BD＝CD ，则四边形 AEDF 是菱形 C、若 AD 垂直平分 BC ，则四边形 AEDF 是矩形 D、若 AD⊥BC ，则四边形 AEDF 是矩形

查看试题解析
8. 如图，在▱ABCD中，AD=2AB，F是AD的中点，E是AB上一点，连接CF、EF、EC，且CF=EF，下列结论正确的个数是（）
①CF平分∠BCD；②∠EFC=2∠CFD；③∠ECD=90°；④CE⊥AB．

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若代数式 $\frac{(x - 2) (x - 1)}{| x | - 1}$ 的值为零，则x的取值应为．

查看试题解析
10. 某校规定学生的期末学科成绩由三部分组成，将课堂、作业和考试三项得分按1：3：6的权重确定每个人的期末成绩.小明同学本学期数学这三项得分分别是：课堂98分，作业95分，考试85分，那么小明的数学期末成绩是分.

查看试题解析
11. 如果x+ $\frac{1}{x}$ ＝3，则 $\frac{x^{2}}{3 x^{4} + x^{2} + 3}$ 的值等于

查看试题解析
12. 如图，△ABC中，∠ACB=90°，∠A=25°，将△ABC绕点C逆时针旋转至△DEC的位置，点B恰好在边DE上，则∠θ=度．

查看试题解析
13. 在菱形ABCD中，对角线AC、BD交于点O，若△ABC的周长为32，BD=16，则菱形ABCD的面积为

查看试题解析
14. 如图，已知△ABC的面积为12，将△ABC沿BC平移到△A'B'C'，使B'和C重合，连接AC'交A'C于D，则△C'DC的面积为

查看试题解析

三、解答题

15. 如图，方格纸上每个小方格的边长都是1，△ABC是通过△A₁B₁C₁旋转得到．

(1)、在图中标出旋转中心点O；

(2)、画出△ABC向下平移4个单位长度，再向右平移4个单位长度得到的△A₂B₂C₂ ．

查看试题解析
16. 因式分解

(1)、a³﹣16a；

(2)、8a²﹣8a³﹣2a

查看试题解析
17. 计算：

(1)、 $\frac{2 a b^{2}}{c}$ +（﹣2bc）× $\frac{c}{a b}$ ；

(2)、先化简，再求值：（ $\frac{2}{x - 1}$ ﹣1）• $\frac{x^{2} - x}{x^{2} - 6 x + 9}$ ，其中x=﹣5．

查看试题解析
18. 解分式方程

(1)、 $\frac{x - 1}{x - 2} = \frac{1}{2 - x} - 2$

(2)、 $\frac{x}{x - 1} - 1 = \frac{3}{(x - 1) (x + 2)}$

查看试题解析
19. 某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．

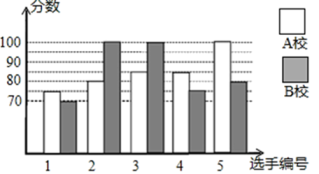(1)、根据图示填写下表：

平均数/分

中位数/分

众数/分

A校

85

B校

85

100

(2)、结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；

(3)、计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．

查看试题解析
20. 如图，在▱ABCD中，G是CD上一点，连接BG且延长交AD的延长线于点E ， AF=CG ， ∠E=30°，∠C=50°，求∠BFD的度数．

查看试题解析
21. 如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

(1)、试判断四边形ADCF的形状，并证明；

(2)、若AB⊥AC，试判断四边形ADCF的形状，并证明．

查看试题解析
22. 小明元旦前到文具超市用15元买了若干练习本，元旦这一天，该超市开展优惠活动，同样的练习本比元旦前便宜0.2元，小明又用20.7元钱买练习本，所买练习本的数量比上一次多50%，小明元旦前在该超市买了多少本练习本？

查看试题解析
23. 如图

(1)、如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA=3，OB=4，OC=5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．求：
①旋转角的度数；

②线段OD的长；

③∠BDC的度数．

(2)、如图2所示，O是等腰直角△ABC（∠ABC=90°）内一点，连接OA、OB、OC，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．当OA、OB、OC满足什么条件时，∠ODC=90°？请给出证明．

查看试题解析
24. 在正方形ABCD中，BD是一条对角线，点P在CD上（与点C，D不重合），连接AP，平移△ADP，使点D移动到点C，得到△BCQ，过点Q作QM⊥BD于M，连接AM，PM（如图1）．

(1)、判断AM与PM的数量关系与位置关系并加以证明；

(2)、若点P在线段CD的延长线上，其它条件不变（如图2），（1）中的结论是否仍成立．请说明理由．

查看试题解析

得分（分）	60	70	80	90	100
人数（人）	7	12	10	8	3

	平均数/分	中位数/分	众数/分
A校		85
B校	85		100