山东省临沂市郯城县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 以下列各组线段的长为边,能组成三角形的是( )A、2、4、7 B、3、5、2 C、7、7、3 D、9、5、32. 下列图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用科学记数法表示:0.000000109是( )A、1.09×10﹣7 B、0.109×10﹣7 C、0.109×10﹣6 D、1.09×10﹣64. 下列各式中,正确的有( )A、 B、 C、 D、a ÷a =a5. 计算 的结果是( )A、 B、-4 C、 D、6. 将分式 中的x、y的值同时扩大2倍,则分式的值( )A、扩大2倍 B、缩小到原来的 C、保持不变 D、无法确定7. 将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( )
3. 用科学记数法表示:0.000000109是( )A、1.09×10﹣7 B、0.109×10﹣7 C、0.109×10﹣6 D、1.09×10﹣64. 下列各式中,正确的有( )A、 B、 C、 D、a ÷a =a5. 计算 的结果是( )A、 B、-4 C、 D、6. 将分式 中的x、y的值同时扩大2倍,则分式的值( )A、扩大2倍 B、缩小到原来的 C、保持不变 D、无法确定7. 将一副直角三角板如图放置,使两直角边重合,则∠α的度数为( ) A、75° B、105° C、135° D、165°8. 若 , ,则 的值为( )A、25 B、 C、9 D、759. 甲、乙两单位为爱心基金分别捐款4800元、6000元,已知甲单位捐款人数比乙单位少50人,而甲单位人均捐款数比乙单位多1元.若设甲单位有x人捐款,则所列方程是( )A、 B、 C、 D、10. 如图, , . , ,垂足分别是点 , ,则 的长是( )
A、75° B、105° C、135° D、165°8. 若 , ,则 的值为( )A、25 B、 C、9 D、759. 甲、乙两单位为爱心基金分别捐款4800元、6000元,已知甲单位捐款人数比乙单位少50人,而甲单位人均捐款数比乙单位多1元.若设甲单位有x人捐款,则所列方程是( )A、 B、 C、 D、10. 如图, , . , ,垂足分别是点 , ,则 的长是( ) A、7 B、3 C、5 D、211. 如果分式方程 无解,则 的值为( )A、-4 B、 C、2 D、-212. 如图, 是等边三角形, ,则 的度数为( )
A、7 B、3 C、5 D、211. 如果分式方程 无解,则 的值为( )A、-4 B、 C、2 D、-212. 如图, 是等边三角形, ,则 的度数为( ) A、50° B、55° C、60° D、65°13. 若等腰 中有一个内角为 ,则这个等腰三角形的一个底角的度数为( )A、 B、 C、 或 D、 或14. 如图, 为 的角平分线, ,过 作 于 , 交 的延长线于 ,则下列结论:① ;② ;③ ;④ 其中正确结论的序号有( )
A、50° B、55° C、60° D、65°13. 若等腰 中有一个内角为 ,则这个等腰三角形的一个底角的度数为( )A、 B、 C、 或 D、 或14. 如图, 为 的角平分线, ,过 作 于 , 交 的延长线于 ,则下列结论:① ;② ;③ ;④ 其中正确结论的序号有( ) A、①②③④ B、②③④ C、①②③ D、①②④
A、①②③④ B、②③④ C、①②③ D、①②④二、填空题
-
15. 分解因式xy2+4xy+4x= .16. 如果多边形的每个内角都等于 ,则它的边数为.17. 已知x2-2(m+3)x+9是一个完全平方式,则m= .18. 阅读材料后解决问题,小明遇到下面一个问题:计算 .经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用方差公式解决问题,具体解法如下: 请你根据小明解决问题的方法,试着解决以下的问题: .
三、解答题
-
19. 如图,∠A=∠D , 要使△ABC≌△DBC , 还需要补充一个条件:(填一个即可).
 20. 解方程:21. 先化简: ÷( ),再从﹣3<x<2的范围内选取一个你最喜欢的整数代入,求值.22. 已知,如图,在 中, 、 分别是 的高和角平分线,若 ,
20. 解方程:21. 先化简: ÷( ),再从﹣3<x<2的范围内选取一个你最喜欢的整数代入,求值.22. 已知,如图,在 中, 、 分别是 的高和角平分线,若 , (1)、求 的度数;(2)、写出 与 的数量关系,并证明你的结论23. 已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
(1)、求 的度数;(2)、写出 与 的数量关系,并证明你的结论23. 已知:方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).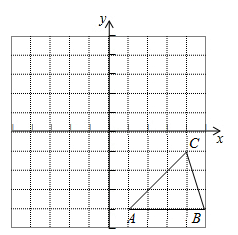 (1)、请以y轴为对称轴,画出与△ABC对称的△A1B1C1 , 并直接写出点A1、B1、C1的坐标;(2)、△ABC的面积是.(3)、点P(a+1,b-1)与点C关于x轴对称,则a= , b=.24. 某内陆城市为了落实国家“一带一路”战略,促进经济发展,增强对外贸易的竞争力,把距离港口490 的普通公路升级成了比原来长度多35 的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2 ,求公路升级以后汽车的平均速度25. 如图,在 中,已知 , 的垂直平分线交 于点 ,交 于点 ,连接
(1)、请以y轴为对称轴,画出与△ABC对称的△A1B1C1 , 并直接写出点A1、B1、C1的坐标;(2)、△ABC的面积是.(3)、点P(a+1,b-1)与点C关于x轴对称,则a= , b=.24. 某内陆城市为了落实国家“一带一路”战略,促进经济发展,增强对外贸易的竞争力,把距离港口490 的普通公路升级成了比原来长度多35 的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2 ,求公路升级以后汽车的平均速度25. 如图,在 中,已知 , 的垂直平分线交 于点 ,交 于点 ,连接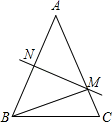 (1)、若 ,则 的度数是度(2)、若 , 的周长是
(1)、若 ,则 的度数是度(2)、若 , 的周长是①求 的长度;
②若点 为直线 上一点,请你直接写出 周长的最小值
26. 如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N. (1)、当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;(2)、将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;(3)、将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.
(1)、当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;(2)、将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△ACN为等腰直角三角形;(3)、将图1中△BCE绕点B旋转到图3位置时,(2)中的结论是否仍成立?若成立,试证明之,若不成立,请说明理由.