山东省临沂市兰陵县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $Δ A B C$ 中， $∠ A : ∠ B : ∠ C = 1 : 2 : 3$ ，则 $∠ A =$ （）

A、 $30 °$ B、 $60 °$ C、 $90 °$ D、 $120 °$

查看试题解析
2. 下列运算中，正确的是（）

A、 $3 a^{2} - a^{2} = 2$ B、 ${(2 a^{2})}^{2} = 2 a^{4}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $a^{3} \cdot a^{2} = a^{5}$

查看试题解析
3. 一副三角板如图摆放，边DE∥AB，则∠1＝（　　）

A、135° B、120° C、115° D、105°

查看试题解析
4. 若 $3^{x} = 4$ ， $9^{y} = 7$ ，则 $3^{x + 2 y}$ 的值为（）

A、 $\frac{4}{7}$ B、 $\frac{7}{4}$ C、28 D、 $\frac{2}{7}$

查看试题解析
5. 计算 $(1 - \frac{1}{x + 1}) \div \frac{x^{2}}{x^{2} - 1}$ 的结果是（）

A、 $x - 1$ B、 $\frac{1}{x}$ C、 $\frac{x - 1}{x}$ D、 $\frac{x}{x - 1}$

查看试题解析
6. 如图，CD是直角△ABC斜边AB上的高，CB＞CA，图中相等的角共有（　　）

A、2对 B、3对 C、4对 D、5对

查看试题解析
7. 如图， $Δ A B C$ 中， $A B = A C$ ，点 $D$ 在 $A C$ 边上，且 $B D = B C = A D$ ，则 $∠ C$ 的度数为（）

A、30° B、36° C、45° D、72°

查看试题解析
8. 如图，在△ABC中，边AC的垂直平分线交边AB于点D，连结CD．若∠A＝50°，则∠BDC的大小为（　　）

A、90° B、100° C、120° D、130°

查看试题解析
9. 张老师和李老师同时从学校出发，步行15千米去县城购买书籍，张老师比李老师每小时多走1千米，结果比李老师早到半小时，两位老师每小时各走多少千米？设李老师每小时走x千米，依题意，得到的方程是（）

A、 $\frac{15}{x + 1} - \frac{15}{x} = \frac{1}{2}$ B、 $\frac{15}{x} - \frac{15}{x + 1} = \frac{1}{2}$ C、 $\frac{15}{x - 1} - \frac{15}{x} = \frac{1}{2}$ D、 $\frac{15}{x} - \frac{15}{x - 1} = \frac{1}{2}$

查看试题解析
10. 如果 $3 x - 4 y = 0$ ，那么代数式 $(\frac{x^{2}}{y} - y) \cdot \frac{3}{x + y}$ 的值为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 如图①，从边长为 $a$ 的正方形中剪去一个边长为 $b$ 的小正方形，然后将剩余部分剪拼成一个长方形（如图②），则上述操作所能验证的公式是（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $a^{2} + a b = a (a + b)$

查看试题解析
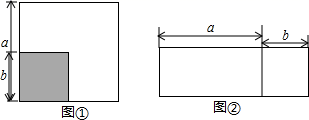12. 如图，在△ABC中，∠C＝90°，AD平分∠CAB ， DE⊥AB于点E ，若DE＝15cm ， BE＝8cm ，则BC的长为（）

A、15cm B、17cm C、30cm D、32cm

查看试题解析
13. 等腰 $△ A B C$ 中， $A B = A C ， ∠ A = 36^{°}$ ，用尺规作图作出线段BD，则下列结论错误的是（）

A、 $A D = B D$ B、 $∠ D B C = 36^{°}$ C、 $S_{Δ A B D} = S_{B C D}$ D、 $△ B C D$ 的周长 $= A B + B C$

查看试题解析
14. 如图，在 $Δ A B C$ 中， $A Q = P Q$ ， $P R = P S$ ， $P R ⊥ A B$ 于 $R$ ， $P S ⊥ A C$ 于 $S$ ，则三个结论① $A S = A R$ ；② $Q P / / A R$ ；③ $Δ B P R ≅ Δ Q P S$ 中，（）

A、全部正确 B、仅①和②正确 C、仅①正确 D、仅①和③正确

查看试题解析

二、填空题

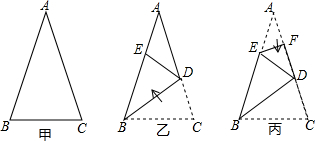
15. 分解因式：3x²-6x+3= ．

查看试题解析
16. 一个n边形的内角和为1080°，则n= ．

查看试题解析
17. 若 $x + y = 2, x - y = 1$ ，则代数式 ${(x + 1)}^{2} - y^{2}$ 的值为.

查看试题解析
18. 已知一张三角形纸片 $A B C ($ 如图甲 $)$ ，其中 $A B = A C .$ 将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为 $B D ($ 如图乙 $) .$ 再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为 $E F ($ 如图丙 $) .$ 原三角形纸片ABC中， $∠ A B C$ 的大小为 $^{\circ} .$

查看试题解析
19. 阅读理解：引入新数 $i$ ，新数 $i$ 满足分配律，结合律，交换律.已知 $i^{2} = - 1$ ，那么 $(1 + i) \cdot (1 - i) =$ .

查看试题解析

三、解答题

20.

(1)、计算： $(\frac{x}{x - 2} - \frac{x}{x + 2}) \div \frac{4 x}{x - 2}$

(2)、解方程： $\frac{x}{x - 2} = \frac{3}{2 x - 4} - 1$

查看试题解析
21. 某服装厂接到一份加工3000件校服的订单．在实际生产之前，接到学校要求需提前供货．该服装厂决定提高加工效率，实际每天加工的件数是原计划的1.2倍，结果提前5天完工，求原计划每天加工校服的件数．

查看试题解析
22. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，延长AE交BC的延长线于点F.

(1)、求证：△DAE≌△CFE；

(2)、若AB＝BC+AD，求证：BE⊥AF.

查看试题解析
23. 如图

(1)、问题原型：如图①，在锐角 $Δ A B C$ 中 $∠ A B C = 45 °$ ， $A D ⊥ B C$ 于点 $D$ ，在 $A D$ 上取点 $E$ ，使 $D E = C D$ ，连结 $B E$ ．求证： $B E = A C$ ．

(2)、问题拓展：如图②，在问题原型的条件下， $F$ 为 $B C$ 的中点，连结 $E F$ 并延长至点 $M$ ，使 $F M = E F$ ，连结 $C M$ ．判断线段 $A C$ 与 $C M$ 的数量关系，并说明理由．

查看试题解析
24. 如图①，点 $O$ 是等边 $Δ A B C$ 内一点， $∠ A O C = 100 °$ ， $∠ A O B = α$ ．以 $O B$ 为边作等边三角形 $B O D$ ，连接 $C D$ ．

(1)、求证： $Δ A B O ≅ Δ C B D$ ；

(2)、当 $α = 150 °$ 时（如图②），试判断 $Δ C O D$ 的形状，并说明理由；

(3)、求当 $α$ 是多少度时， $Δ C O D$ 是等腰三角形？（写出过程）

查看试题解析