山东省菏泽市牡丹区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、-2 B、2 C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
2. 在实数 $- \frac{1}{5}$ ， ${}^{3}{\sqrt{- 27}}$ ， $\frac{π}{2}$ ， $\sqrt{16}$ ， $\sqrt{8}$ ，0中，无理数的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知点 $M$ 到 $x$ 轴的距离为 $3$ ，到 $y$ 轴距离为 $2$ ，且在第二象限内，则点 $M$ 的坐标为（）

A、 $(- 2, 3)$ B、 $(2, 3)$ C、 $(- 3, 2)$ D、不能确定

查看试题解析
4. 下列条件中，不能判断 $Δ A B C$ 是直角三角形的是（）

A、 $a : b : c = 3 : 4 : 5$ B、 $a : b : c = 1 : 2 : \sqrt{3}$ C、 $∠ A + ∠ B = ∠ C$ D、 $∠ A : ∠ B : ∠ C = 3 : 4 : 5$

查看试题解析
5. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1=25°，则∠2的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
6. 小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法错误的是（）．

A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是

查看试题解析
7. 一次函数 $y = k x + b$ 满足 $k b < 0$ ，且y随x的增大而减小，则此函数的图象一定不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 已知，如图点A（1，1），B（2，﹣3），点P为x轴上一点，当|PA﹣PB|最大时，点P的坐标为（）

A、（﹣1，0） B、（ $\frac{1}{2}$ ，0） C、（ $\frac{5}{4}$ ，0） D、（1，0）

查看试题解析

二、填空题

9. 要使 $\sqrt{x - 2}$ 在实数范围内有意义，x应满足的条件是．

查看试题解析
10. 已知函数y=(m+2)x^|m+3| ，当m=时，此函数为正比例函数。

查看试题解析
11. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，则k的值是．

查看试题解析
12. 如图，长方体的长为 $15$ ，宽为 $10$ ，高为 $20$ ，点 $B$ 离点 $C$ 的距离为 $5$ ，一只蚂蚁如果要沿着长方体的表面从点 $A$ 爬到点 $B$ ，需要爬行的最短距离是。

查看试题解析
13. 一次函数 $y = 3 x + b$ 和 $y = a x - 3$ 的图像如图所示，其交点为 $P (- 2 ， - 5)$ ，则不等式 $(3 - a) x + b + 3 < 0$ 的解集是．

查看试题解析
14. 如图，在平面直角坐标系中，长方形ABCO的边COOA分别在x轴，y轴上，点E在边BC上，将该长方形沿AE折叠，点B恰好落在边OC上的点F处，若OA=8，CF=4，则AE所在直线的表达式为。

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{48} - \sqrt{27} + \sqrt{\frac{1}{3}}$

(2)、 $\frac{\sqrt{8} + \sqrt{18}}{\sqrt{2}} - {(3 \sqrt{2} - 1)}^{2}$

查看试题解析
16. 用合适的方法解方程组：

(1)、 ${\begin{matrix} x = 2 y \\ 2 x - 3 y = 2 \end{matrix}$

(2)、 ${\begin{matrix} 3 x + 2 y = 3 \\ 5 x - 6 y = - 23 \end{matrix}$ .

查看试题解析
17. 已知：如图，点E在直线DF上，点B在直线AC上， $∠ 1 = ∠ 2 ， ∠ 3 = ∠ 4$ .
求证： $∠ A = ∠ F$

查看试题解析
18. 某农场去年生产大豆和小麦共300吨。采用新技术后，今年总产量为350吨，与去年相比较，大豆超产10%，小麦超产20%。求该农场今年实际生产大豆和小麦各多少吨?

查看试题解析
19. 织金县某中学300名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵.将各类的人数绘制成扇形图（如图1）和条形图（如图2）.
回答下列问题：

(1)、在这次调查中D类型有多少名学生？

(2)、写出被调查学生每人植树量的众数、中位数；

(3)、求被调查学生每人植树量的平均数，并估计这300名学生共植树多少棵？

查看试题解析
20. 探究与发现：如图1所示的图形，像我们常见的学习用品—圆规．我们不妨把这样图形叫做“规形图”．

(1)、观察“规形图”，试探究 $∠ B D C$ 与 $∠ A$ 、 $∠ B$ 、 $∠ C$ 之间的关系，并说明理由；

(2)、请你直接利用以上结论，解决以下三个问题：
①如图2，把一块三角尺 $X Y Z$ 放置在 $Δ A B C$ 上，使三角尺的两条直角边 $X Y$ 、 $X Z$ 恰好经过点 $B$ 、 $C$ ， $∠ A = 40 °$ ，则 $∠ A B X + ∠ A C X =$ ；

②如图3， $D C$ 平分 $∠ A D B$ ， $E C$ 平分 $∠ A E B$ ，若 $∠ D A E = 40 °$ ， $∠ D B E = 130 °$ ，求 $∠ D C E$ 的度数；

③如图4， $∠ A B D$ ， $∠ A C D$ 的 $8$ 等分线相交于点 $G_{1}$ ， $G_{2}$ ， $G_{3}$ ， $\dots$ $G_{7}$ ，若 $∠ B D C = 130 °$ ， $∠ B G_{1} C = 60 °$ ，求 $∠ A$ 的度数．

查看试题解析
21.
小明和爸爸从家步行去公园，爸爸先出发一直匀速前行，小明后出发．家到公园的距离为2500m，如图是小明和爸爸所走的路程s（m）与步行时间t（min）的函数图象．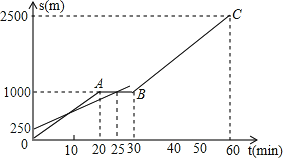

(1)、直接写出小明所走路程s与时间t的函数关系式；

(2)、小明出发多少时间与爸爸第三次相遇？

(3)、在速度都不变的情况下，小明希望比爸爸早20min到达公园，则小明在步行过程中停留的时间需作怎样的调整？

查看试题解析