山东省德州市陵城区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{2} + a^{2} = a^{4}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
2. 对称现象无处不在，请你观察下面的四个图形，它们体现了中华民族的传统文化，其中，可以看作是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在 $- 2 a, \frac{1}{a - b}, \frac{a + b}{2}, \frac{3}{π} ， \frac{1}{x^{2} - 1}, - \frac{2}{5}, x + \frac{1}{x}, \frac{x^{2} - 1}{x + 1}$ ，分式的个数有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
4. 如图，在△ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E、 F为AB上的一点，CF⊥AD于H，下列判断正确的有（）

A、AD是△ABE的角平分线 B、BE是△ABD边AD上的中线 C、AH为△ABC的角平分线 D、CH为△ACD边AD上的高

查看试题解析
5. 如图，△ABC中，∠C=90°，AC=BC，AD是∠BAC的平分线，DE⊥AB，垂足为E，若AB=10cm，则△DBE的周长等于（）

A、10cm B、8cm C、12cm D、9cm

查看试题解析
6. 小明想用一长方形的硬纸片折叠成一个无盖长方体收纳盒，硬纸片长为a+1，宽为a-1，如图，在硬纸片的四角剪裁出4个边长为1的正方形，沿着图中虚线折叠，这个收纳盒的体积是（）

A、a² -1 B、a²-2a C、a²-1 D、a²-4a+3

查看试题解析
7. 下列各式从左到右的变形属于分解因式的是（）

A、 $(a - 1) (a + 1) = a^{2} - 1$ B、 $x^{2} - 4 = (x - 2) (x + 2)$ C、 $x^{2} - 4 + 3 x = (x + 2) (x - 2) + 3 x$ D、 $x^{2} - 1 = x (x - \frac{1}{x})$

查看试题解析
8. 如图，△ABD≌△CDB，且AB，CD是对应边．下面四个结论中错误的是（）

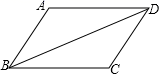A、△ABD和△CDB的面积相等 B、△ABD和△CDB的周长相等 C、∠A+∠ABD=∠C+∠CBD D、AD∥BC，且AD=BC

查看试题解析
9. 如果4 x²—a x+9是一个完全平方式，则a的值是（）

A、+6 B、6 C、12 D、+12

查看试题解析
10. 若一个等腰三角形腰上的高等于腰长的一半，则这个等腰三角形底角度数为（）

A、30° B、30°或60° C、15°或30° D、15°或75°

查看试题解析
11. 某工程队在城区内铺设一条长4000米的管道，为尽量减少施工对交通造成的影响，施工时“……”，设实际每天铺设管道x米，则可得方程 $\frac{4000}{x - 12} - \frac{4000}{x} = 20$ ，根据此情景，题中用“……”表示的缺失的条件应补为（）

A、每天比原计划多铺设12米，结果延期20天完成 B、每天比原计划少铺设12米，结果延期20天完成 C、每天比原计划多铺设12米，结果提前20天完成 D、每天比原计划少铺设12米，结果提前20天完成

查看试题解析
12. 如图，给正五边形的顶点依次编号为1，2，3，4，5．若从某一顶点开始，沿正五边形的边顺时针方向行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”，如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点，然后从1→2为第二次“移位”．若小宇从编号为4的顶点开始，第2020次“移位”后，则他所处顶点的编号为（）．

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 多项式 ${(x - 5)}^{2} - 5^{2}$ 因式分解为

查看试题解析
14. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值为．

查看试题解析
15. 已知 $P_{1}$ (a−1，5)和 $P_{2}$ (2，b−1)关于x轴对称，则 $- {(a + b)}^{2020}$ 的值为．

查看试题解析
16. 小明同学在计算一个多边形(每个内角小于180°)的内角和时，由于粗心少算一个内角，结果得到的和是2020°，则少算了这个内角的度数为．

查看试题解析
17. 如图，点P是∠AOB内任意一点，且∠AOB=40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为．

查看试题解析
18. 若数m使关于x的不等式组 ${\begin{array}{l} x - 2 \leq - x + 4 \\ 7 x + 4 > - m \end{array}$ 有且仅有四个整数解，且使关于x的分式方程 $\frac{m}{2 - x} - 1 = \frac{x}{x - 2}$ 有非负数解，则所有满足条件的整数m的值之和是．

查看试题解析

三、解答题

19. 计算

(1)、 ${(- 3 x y)}^{2} \cdot y^{2} - {(- 2 x y^{2})}^{2} + {(- 2 x y^{2})}^{3} \div 2 x y^{2}$

(2)、 $(a - b + 2) (a + b + 2)$

(3)、 $45^{2} + 55^{2} - 110 \times 45$

查看试题解析
20. 先化简，再求值．
$(1 + \frac{x^{2} + 2}{x - 2}) \div \frac{x + 1}{x^{2} - 4 x^{} + 4}$ ，其中x满足 $x^{2} - 2 x + 5 = 0$ ．

查看试题解析
21. 解分式方程 $\frac{x}{x - 1} = \frac{2}{x^{2} - 1} + 1$

查看试题解析
22. 如图在△ABC中，∠B=50°，∠C=30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，连接AD，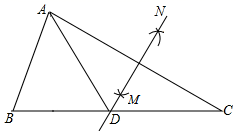

(1)、若△ABD的周长是19，AB=7，求BC的长；

(2)、求∠BAD的度数．

查看试题解析
23. 如图，在△ABC中，AE为∠BAC的角平分线，点D为BC的中点，DE⊥BC交AE于点E，EG⊥AC于点G．

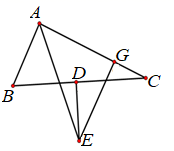(1)、求证： AB+AC=2AG．

(2)、若BC=8cm，AG=5cm，求△ABC的周长．

查看试题解析
24. 节日里，兄弟两人在60米的跑道上进行短距离比赛，两人从出发点同时起跑，哥哥到达终点时，弟弟离终点还差12米．

(1)、若哥哥的速度为10米/秒，
①求弟弟的速度；

②如果两人重新开始比赛，哥哥从起点向后退10米，兄弟同时起跑，两人能否同时到达终点？若能，请求出两人到达终点的时间；若不能，请说明谁先到达终点．

(2)、若哥哥的速度为m米/秒，
①弟弟的速度为米/秒(用含m的代数式表示)；

②如果两人想同时到达终点，哥哥应向后退多少米？

查看试题解析
25. 已知 $Δ A B C$ 为等边三角形，点 $D$ 为直线 $B C$ 上一动点(点 $D$ 不与点 $B$ 、点 $C$ 重合)．连接 $A D$ ，以 $A D$ 为边向逆时针方向作等边 $Δ A D E$ ，连接 $C E$ ，

(1)、如图1，当点 $D$ 在边 $B C$ 上时：
求证： $Δ A B D ≌ Δ A C E$ ；

(2)、判断 $A C 、 C D 、 C E$ 之间的数量关系是；

(3)、如图2，当点 $D$ 在边 $B C$ 的延长线上时，其他条件不变，判断 $A C 、 C D 、 C E$ 之间存在的数量关系，并写出证明过程；

(4)、如图3，当点 $D$ 在边 $B C$ 的反向延长线上时，其他条件不变，请直接写出 $A C 、 C D 、 C E$ 之间存在的数量关系为．

查看试题解析