山东省德州市临邑县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 如果一个多边形的内角和是外角和的5倍,那么这个多边形的边数是( )A、11 B、12 C、13 D、142. 已知三角形的两边分别为1和4,第三边长为整数 ,则该三角形的周长为( )A、7 B、8 C、9 D、103. 将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )。
 A、45° B、60° C、75° D、85°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,点 与点 关于y轴对称,则( )A、 , B、 , C、 , D、 ,7. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A、45° B、60° C、75° D、85°4. 下列运算正确的是( )A、 B、 C、 D、5. 下列因式分解正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,点 与点 关于y轴对称,则( )A、 , B、 , C、 , D、 ,7. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )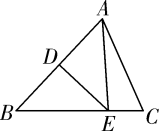 A、8 B、11 C、16 D、178. 下列各式不成立的是( )A、 B、 C、 D、9. 如果 ,那么代数式 的值为( )A、-3 B、-1 C、1 D、310. 如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( )
A、8 B、11 C、16 D、178. 下列各式不成立的是( )A、 B、 C、 D、9. 如果 ,那么代数式 的值为( )A、-3 B、-1 C、1 D、310. 如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E。若DE=1,则BC的长为( ) A、2+ B、 C、 D、311. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、12. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ).
A、2+ B、 C、 D、311. 为推进垃圾分类,推动绿色发展.某化工厂要购进甲、乙两种型号机器人用来进行垃圾分类.用 万元购买甲型机器人和用 万元购买乙型机器人的台数相同,两型号机器人的单价和为 万元.若设甲型机器人每台 万元,根据题意,所列方程正确的是( )A、 B、 C、 D、12. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ). A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
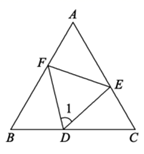
13. 因式分解: .14. 若 ,则 的值为 .15. 如图,在等腰三角形 中, , 为 边上中点,过 点作 ,交 于 ,交 于 ,若 ,则 的长为 .
 16. 计算: 的结果是 .17. 已知关于x的分式方程 的解为正数,则 的取值范围为 .18. 如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为 .
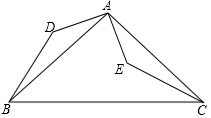
16. 计算: 的结果是 .17. 已知关于x的分式方程 的解为正数,则 的取值范围为 .18. 如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A,C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为 .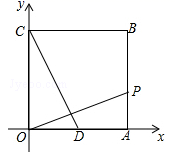 19. 如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是 .
19. 如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是 .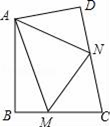
三、解答题
-
20. 按要求计算:(1)、计算:(2)、因式分解:①
②
(3)、解方程:21. 先化简,再求值 ,其中 满足
22. 如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. (1)、在图中画出与 关于直线 成轴对称的 ;(2)、在直线 上找一点 ,使 的值最小;(3)、若 是以 为腰的等腰三角形,点 在 图中小正方形的顶点上.这样的点 共有个.(标出位置)23. 如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.
(1)、在图中画出与 关于直线 成轴对称的 ;(2)、在直线 上找一点 ,使 的值最小;(3)、若 是以 为腰的等腰三角形,点 在 图中小正方形的顶点上.这样的点 共有个.(标出位置)23. 如图,AB=AC,AB⊥AC,AD⊥AE,且∠ABD=∠ACE.求证:BD=CE.