山东省烟台市莱山区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-12-07 类型:期末考试
一、单选题
-
1. 4的算术平方根是( )A、 B、2 C、±2 D、±2. 下列各数,﹣3,π,﹣ ,0, ,0.010010001…(每相邻两个1之间0的个数依次多1),其中无理数的个数是( )A、1 B、2 C、3 D、43. 下列智能手机的功能图标中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
4. 在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是( )
A、(4,1) B、(﹣1,4) C、(﹣4,﹣1) D、(﹣1,﹣4)5. 如图,若用我们数学课本上采用的科学计算器进行计算,其按键顺序为 ,则输出结果应为( ) A、8 B、4 C、 D、6. 如果 =﹣ ,那么a,b的关系是( )A、a=b B、a=±b C、a=﹣b D、无法确定7. 若函数 的值随自变量的增大而增大,则函敷 的图象大致是( )A、
,则输出结果应为( ) A、8 B、4 C、 D、6. 如果 =﹣ ,那么a,b的关系是( )A、a=b B、a=±b C、a=﹣b D、无法确定7. 若函数 的值随自变量的增大而增大,则函敷 的图象大致是( )A、 B、
B、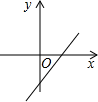 C、
C、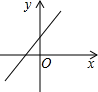 D、
D、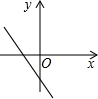 8. 如图,已知△ABC中,AB=AC,∠C=65°.ED垂直平分AB,分别交AB,AC于点E,D,那么∠DBC的度数为( )
8. 如图,已知△ABC中,AB=AC,∠C=65°.ED垂直平分AB,分别交AB,AC于点E,D,那么∠DBC的度数为( ) A、10° B、15° C、20° D、25°9. 小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是( )
A、10° B、15° C、20° D、25°9. 小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1mm,则图中转折点P的坐标表示正确的是( ) A、(5,30) B、(8,10) C、(9,10) D、(10,10)10. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、(5,30) B、(8,10) C、(9,10) D、(10,10)10. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( ) A、( ,1) B、(2,1) C、(2, ) D、(1, )11. 如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═ ∠BAC,则DE的长为( )
A、( ,1) B、(2,1) C、(2, ) D、(1, )11. 如图,等腰△ABC中,AB=AC=10cm,BC=12cm,D为BC上一点,连接AD,E为AD上一点,连接BE,若∠ABE=∠BAE═ ∠BAC,则DE的长为( ) A、 cm B、 cm C、 cm D、1cm12. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( )
A、 cm B、 cm C、 cm D、1cm12. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=3cm,点P在边AC上以1cm/s的速度从点A向终点C运动,与此同时点Q在边AB上以同样的速度从点B向终点A运动,各自到达终点后停止运动,设运动时间为t(s),则当△APQ是直角三角形时,t的值为( ) A、2s B、4s C、2s或4s D、2s或4.5s
A、2s B、4s C、2s或4s D、2s或4.5s二、填空题
-
13. 点P(2-a,a+1)在y轴上,则a=。
14. 小明将一张正方形纸片按如图所示顺序折叠成纸飞机,当机翼展开在同一平面时(机翼间无缝隙), 的度数是. 15. 某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:
15. 某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:t(小时)
0
1
2
3
y(升)
120
112
104
96
由表格中y与t的关系可知,当汽车行驶小时,油箱的余油量为0.
16. 已知点A(﹣2,y1),B(1,y2)在直线y=kx+b上,且直线经过第一、二、四象限,则y1y2 . (用“>”,“<”或“=”连接)17. 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行,且经过点A(1,﹣2),则kb= .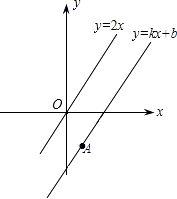 18. 如图,已知△ABC的周长是10cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=0.8cm,△ABC的面积为cm2 .
18. 如图,已知△ABC的周长是10cm,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=0.8cm,△ABC的面积为cm2 . 19. 如图,数轴上表示1, 的对应点分别为A、B,B点关于点A的对称点为点C,则点C所对应的数为 .
19. 如图,数轴上表示1, 的对应点分别为A、B,B点关于点A的对称点为点C,则点C所对应的数为 . 20. 如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点A1 , A2 , A3 , …在直线l上,点B1 , B2 , B3…在x轴的正半轴上,若△A1OB1 , △A2B1B2 , △A3B2B3 , …,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn , 顶点Bn的坐标为 .
20. 如图,在平面直角坐标系中,直线l:y=x+1交x轴于点A,交y轴于点A1 , A2 , A3 , …在直线l上,点B1 , B2 , B3…在x轴的正半轴上,若△A1OB1 , △A2B1B2 , △A3B2B3 , …,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn , 顶点Bn的坐标为 .
三、解答题
-
21. 计算:( +1)0+ ﹣(﹣ )222. 已知:四边形ABCD.
求作:点P,使∠PCB=∠B,且点P到边AD和CD的距离相等.
 23. △ABC是等边三角形,D是AC上一点,BD=CE , ∠1=∠2,试判断BC与AE的位置关系,并证明你的结论.
23. △ABC是等边三角形,D是AC上一点,BD=CE , ∠1=∠2,试判断BC与AE的位置关系,并证明你的结论. 24. 已知一个正数m的平方根为2n+1和5﹣3n.(1)、求m的值;(2)、|a﹣3|+ +(c﹣n)2=0,a+b+c的立方根是多少?25. 计算下列各式:(1)、 =;(2)、 =;(3)、 =;(4)、 =;(5)、 =;(6)、猜想 = . (用含n的代数式表示)26. 如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题:
24. 已知一个正数m的平方根为2n+1和5﹣3n.(1)、求m的值;(2)、|a﹣3|+ +(c﹣n)2=0,a+b+c的立方根是多少?25. 计算下列各式:(1)、 =;(2)、 =;(3)、 =;(4)、 =;(5)、 =;(6)、猜想 = . (用含n的代数式表示)26. 如图,正方形ABCD的边长为4cm,动点P从A点出发,在正方形的边上沿A→B→C→D运动,设运动的时间为t(s),△APD的面积为S(cm2),S与t的函数图象如图所示,请回答下列问题: (1)、点P在AB上运动时间为s,在CD上运动的速度为cm/s,△APD的面积S的最大值为cm2;(2)、将S与t之间的函数关系式补充完整S= ;(3)、请求出运动时间t为几秒时,△APD的面积为6cm2 .27. 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)、点P在AB上运动时间为s,在CD上运动的速度为cm/s,△APD的面积S的最大值为cm2;(2)、将S与t之间的函数关系式补充完整S= ;(3)、请求出运动时间t为几秒时,△APD的面积为6cm2 .27. 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处. (1)、求直线AB的表达式;(2)、求点C和点D的坐标;(3)、y轴的正半轴上是否存在一点P,使得S△PAB= S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.28. 如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿 路径向终点B运动,点Q从B点出发,沿 路径向终点A运动.点P 和Q分别 和 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.
(1)、求直线AB的表达式;(2)、求点C和点D的坐标;(3)、y轴的正半轴上是否存在一点P,使得S△PAB= S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.28. 如图所示,△ABC中,∠ACB=90°,AC=6cm,BC =8cm.点P从A点出发,沿 路径向终点B运动,点Q从B点出发,沿 路径向终点A运动.点P 和Q分别 和 的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过点P和Q作PE⊥l于E,QF⊥l于F.则点P运动多少秒时,△PEC和△CFQ全等?请说明理由.

