山东省潍坊诸城市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 为了了解某市七年级8万名学生的数学学习情况，抽查了10%的学生进行一次测试成绩分析.下面四个说法中，正确的是（）

A、8000名学生是总体 B、8000名学生的测试成绩是总体的一个样本 C、每名学生是总体的一个样本 D、样本容量是80000

查看试题解析
2. 下列说法正确的是（）

A、单项式 $- \frac{x^{2}}{2}$ 的系数是-1 B、单项式 $π a b$ 的次数是3 C、 $\frac{1}{a}$ 和 $\frac{a}{4}$ 都是整式 D、多项式 $4 - a b x + 2 x y^{3}$ 是四次三项式

查看试题解析
3. 已知一辆汽车在 $a$ 秒内行驶了 $\frac{m}{3}$ 米，则它在4分钟内行驶（）

A、 $\frac{4 m}{3}$ 米 B、 $\frac{80 m}{a}$ 米 C、 $\frac{40 m}{a}$ 米 D、 $\frac{480 m}{a}$ 米

查看试题解析
4. 如图，点C、D为线段AB上两点，AC+BD=a ，且AD+BC= $\frac{3}{2}$ AB ，则CD等于（）

A、2a B、A C、 $\frac{2}{3} a$ D、 $\frac{3}{5} a$

查看试题解析
5. 现有两堆棋子，将第一堆中的3枚棋子移动到第二堆后，第二堆的棋子数是第一推棋子的3倍.设第一堆原有 $m$ 枚棋子，则第二堆的棋子原有枚数为（）

A、 $3 m - 6$ B、 $3 m - 3$ C、 $\frac{m + 3}{3}$ D、 $3 m - 12$

查看试题解析
6. 定义一种新的运算： $a \otimes b = a b - a$ ，如 $2 \otimes 3 = 2 \times 3 - 2 = 4$ ，则 $(- 1) \otimes [(- 2) \otimes 5]$ 等于（）

A、13 B、11 C、9 D、7

查看试题解析
7. 已知单项式 $3 x^{a + 1} y^{4}$ 与 $- 2 y^{b - 2} x^{3}$ 是同类项，则下列单项式中，与它们是同类项的是（）

A、 $- 5 x^{b - 3} y^{4}$ B、 $3 x^{b} y^{4}$ C、 $x^{a} y^{4}$ D、 $- x^{a} y^{b + 1}$

查看试题解析
8. 在解方程 $\frac{2 x + 1}{3} - \frac{10 x + 1}{6} = 1$ 时，去分母的过程正确的是（）

A、 $2 x + 1 - (10 x + 1) = 1$ B、 $4 x + 1 - 10 x + 1 = 6$ C、 $2 (2 x + 1) - (10 x + 1) = 1$ D、 $4 x + 2 - 10 x - 1 = 6$

查看试题解析
9. 下列关于变量x，y的关系，其中y不是x的函数的是（）

A、 B、 C、 D、

查看试题解析
10. 某商场今年 $1 ~ 5$ 月的商品销售总额一共是 $410$ 万元，如图（1）表示的是其中每个月销售总额的情况，图（2）表示的是商场服装部各月销售额占商场当月销售总额的百分比情况，观察图（1）、图（2），下列说法错误的是（）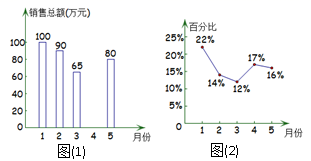

A、4月份商场的商品销售总额是75万元 B、1月份商场服装部的销售额是22万元 C、5月份商场服装部的销售额比4月份减少了 D、3月份商场服装部的销售额比2月份减少了

查看试题解析
11. 如图，数轴上的点 $A ， B ， C ， D$ 对应的数分别是整数 $a ， b ， c ， d$ ，且 $b - 2 a = 3 c + d + 21$ ，那么数轴上原点对应的点是（）

A、A点 B、B点 C、C点 D、D点

查看试题解析
12. 如图是由从1开始的连结自然数组成，按此规律继续写下去，则前8行所有自然数的和与第10行最后一个数分别是（）

A、2080，100 B、4160，64 C、5050，100 D、2525，64

查看试题解析

二、填空题

13. 一个正方形的边长增加 $3.5 c m$ 后，得到的新正方形的周长是 $38 c m$ ，则原来正方形的面积等于．

查看试题解析
14. 已知关于 $x$ 的函数 $y = (a - 1) x + 2 a - 4$ ，当 $x = - 1$ 时， $y = 0$ .那么，当函数值等于 $- 10$ 时，自变量的取值为．

查看试题解析
15. 图1和图2中所有的正方形都相同，将图1的正方形放在图2中的（从①、②、③、④中选填所有可能）位置，所组成的图形能够围成正方体.

查看试题解析
16. 已知有理数 $a ， b ， c$ 满足 $a + b + c = 0$ ，且 $a b c \neq 0$ ，那么 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} + \frac{| a b c |}{a b c}$ 的值等于．

查看试题解析
17. 有一种24点的游戏，游戏规则是：任取四个 $1 \sim 13$ 之间的自然数，将这四个数（每个数只用一次）进行加减乘除四则运算，使其结果等于24，例如对1、2、3、4可做运算： $(1 + 2 + 3) \times 4 = 24$ .现有四个有理数7，-2，3，-4，运用上述规则写出算式，使其运算结果等于24，你的算式是．

查看试题解析
18. 如图是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，依此规律.第n个图案中有个涂有阴影的小正方形(用含有n的代数式表示)

查看试题解析

三、解答题

19. 计算

(1)、 $(- \frac{1}{2} - \frac{1}{3}) \div \frac{5}{4} \times \frac{6}{5}$ ．

(2)、 $- 0.4 \div \frac{11}{5} - \frac{6}{21} \times (- \frac{7}{4}) - 0.25$ ．

查看试题解析
20. 解方程

(1)、 $3 x - 4 (2 x + 5) = 7 (x - 5) + 4 (2 x + 1)$ ．

(2)、 $\frac{y - 1}{2} - 2 = - y - \frac{y + 2}{5}$ ．

查看试题解析
21. 为了更好地利用“大课间”加强学生的体育锻炼，调动学生运动的积极性，某初中学校围绕着“你最喜欢的体育活动项目是什么（只写一项）？”的问题，对在校学生进行了随机抽样调查，得到一组数据，绘制如图所示统计图表：

(1)、该校对多少名学生进行了抽样调查？

(2)、求图2中“抖空竹”运动项目所对应的图形区域的圆心角度数，并分别在图1和图2中将“抖空竹”部分的图形补充完整；

(3)、已知该校八年级学生占全校总学生数的 $\frac{1}{3}$ ，九年级学生占全校学生数的 $\frac{8}{25}$ ，七年级的有520名学生请你利用样本数据统计全校学生中最喜欢踢毽子运动的人数约为多少？

查看试题解析
22. 甲三角形的周长为 $3 a^{2} - 6 b + 8$ ，乙三角形的第一条边长为 $a^{2} - 2 b$ ，第二条边长为 $a^{2} - 3 b$ ，第三条边比第二条边短 $a^{2} - 2 b - 5$ ．

(1)、求乙三角形第三条边的长；

(2)、甲三角形和乙三角形的周长哪个大？试说明理由．

查看试题解析
23. 公司生产一种电脑耗材，每件成本价是400元，销售价为510元，本季度销售了5万件．经过市场调研，预计下一季度这种电脑耗材每件销售价会降低4%，销售量将提高10%．

(1)、求下一季度每件电脑耗材的销售价和销售量；

(2)、为进一步扩大市场，公司决定降低生产成本，要使销售利润（销售利润=销售价-成本价）保持不变，每件电脑耗材的成本价应降低多少元？

查看试题解析
24. 根据材料，解答问题
如图，数轴上有点 $A ， B ， C ， D$ ，对应的数分别是6，-4，4，-1，则 $A ， C$ 两点间的距离为 $| 6 - 4 | = 2$ ； $B ， D$ 两点间的距离为 $| - 1 - (- 4) | = 3$ ； $A ， B$ 两点间的距离为 $| 6 - (- 4) | = 10$ ；由此，若数轴上任意两点 $E ， F$ 分别表示的数是 $e ， f$ ，则 $E 、 F$ 两点间的距离可表示为 $| e - f |$ ．反之， $| e - f |$ 表示有理数 $e 、 f$ 在数轴上的对应点 $E 、 F$ 之间的距离，称之为绝对值的几何意义．

(1)、问题应用1：
如果表示-1的点 $D$ 和表示 $m$ 的点 $P$ 之间的距离是2，则点 $P$ 对应的 $m$ 的值为；

(2)、方程 $| m + 3 | = 4$ 的解 $m =$ ；

(3)、方程 $| m + 4 | = | m - 6 |$ 的解 $m =$ ；

(4)、问题应用2：
如图，若数轴上表示 $n$ 的点为 $Q$ .

$| n - 4 |$ 的几何意义是数轴上，当 $n =$ ， $| n - 4 |$ 的值最小是；

(5)、 $| n + 1 | + | n - 4 |$ 的几何意义是数轴上， $| n + 1 | + | n - 4 |$ 的最小值是，此时点 $Q$ 在数轴上应位于上；

(6)、根据以上推理方法可求 $| n - 1 | + | n - 2 | + | n - 3 |$ 的最小值是，此时 $n =$ ．

查看试题解析