山东省临沂市费县2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-07 类型：期末考试

进入出卷网下载

一、单选题

1. 国家体育场“鸟巢”的建筑面积达258000m² ，用科学记数法表示为（）

A、25.8×10⁵ B、2.58×10⁵ C、2.58×10⁶ D、0.258×10⁷

查看试题解析
2. 下列各式中运算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $4 a - 3 a = 1$ C、 $3 a^{2} b - 4 {ba}^{2} = - a^{2} b$ D、 $3 a^{2} + 2 a^{3} = 5 a^{5}$

查看试题解析
3. 如果以x＝－5为方程的解构造一个一元一次方程，那么下列方程中不满足要求的是（）

A、x＋5＝0 B、x－7＝－12 C、2x＋5＝－5 D、 $- \frac{x}{5}$ ＝－1

查看试题解析
4. 如图，将正方体的平面展开图重新折成正方体后，“祝”字对面的字是（）

A、新 B、年 C、快 D、乐

查看试题解析
5. $a - (b - c)$ 去括号正确的是（）

A、 $a - b - c$ B、 $a + b - c$ C、 $a - b + c$ D、 $a + b + c$

查看试题解析
6. 如图：A、B、C、D四点在一条直线上，若AB＝CD，下列各式表示线段AC错误的是（）

A、AC＝AD﹣CD B、AC＝AB+BC C、AC＝BD﹣AB D、AC＝AD﹣AB

查看试题解析
7. 将一副三角板按照如图所示的位置摆放，则图中的 $∠ α$ 和 $∠ β$ 的关系一定成立的是（）

A、互余 B、互补 C、相等 D、无法确定

查看试题解析
8. 下列等式变形正确的是（）.

A、如果mx＝my，那么x＝y B、如果︱x︱＝︱y︱，那么x＝y C、如果－ $\frac{1}{2}$ x＝8，那么x＝－4 D、如果x－2＝y－2，那么x＝y

查看试题解析
9. 在解方程 $\frac{x}{3} = 1 - \frac{x - 1}{5}$ 时，去分母后正确的是（）

A、 $5 x = 15 - 3 (x - 1)$ B、 $5 x = 1 - (3 x - 1)$ C、 $5 x = 1 - 3 (x - 1)$ D、 $5 x = 3 - 3 (x - 1)$

查看试题解析
10. 在灯塔O处观测到轮船A位于北偏西54°的方向，同时轮船B在南偏东15°的方向，那么∠AOB的大小为（）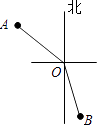

A、69° B、111° C、141° D、159°

查看试题解析
11. 若一个角的补角的余角是28°，则这个角的度数为（）

A、128° B、118° C、72° D、62°

查看试题解析
12. 一件夹克衫先按成本价提高50%标价，再将标价打8折出售，结果获利28元，如果设这件夹克衫的成本价是x元，那么根据题意，所列方程正确的是（）

A、 $0.8 (1 + 0.5) x = x + 28$ B、 $0.8 (1 + 0.5) x = x - 28$ C、 $0.8 (1 + 0.5 x) = x - 28$ D、 $0.8 (1 + 0.5 x) = x + 28$

查看试题解析
13. 轮船沿江从A港顺流行驶到B港，比从B港返回A港少用3小时，若船速为26千米/时，水速为2千米/时，求A港和B港相距多少千米．设A港和B港相距x千米．根据题意，可列出的方程是（）

A、 $\frac{x}{28} = \frac{x}{24} - 3$ B、 $\frac{x}{28} = \frac{x}{24} + 3$ C、 $\frac{x + 2}{26} = \frac{x - 2}{26} + 3$ D、 $\frac{x - 2}{26} = \frac{x + 2}{26} - 3$

查看试题解析
14. 如图，下列图形中的数字按一定规律排列按此规律，则第 $6$ 个图中 $m$ 的值为（）

A、 $\frac{3}{8}$ B、 $\frac{7}{36}$ C、 $\frac{11}{48}$ D、 $\frac{13}{96}$

查看试题解析

二、填空题

15. 一元一次方程 $2 x + 6 = 0$ 的解为 $x =$ ．

查看试题解析
16. 计算 $- 2^{3} - 4 \times \frac{1}{4} =$ ．

查看试题解析
17. 若数轴上点 $A$ 和点 $B$ 分别表示数 $- 3$ 和 $1$ ，则点 $A$ 和点 $B$ 之间的距离是．

查看试题解析
18. 已知线段 $AB = 10 cm$ ，点D是线段AB的中点，直线AB上有一点C，并且 $BC = 2$ cm，则线段 $DC =$ ．

查看试题解析
19. 如图，将长方形纸片 $A B C D$ 沿直线 $E N$ ， $E M$ 进行折叠后（点 $E$ 在 $A B$ 边上）， $B^{'}$ 点刚好落在 $A^{'} E$ 上，若折叠角 $∠ A E N = 32 °$ ，则另一个折叠角 $∠ B E M =$ ．

查看试题解析

三、解答题

20. 解下列方程：

(1)、 $3 x - 3 = 4 x + 5$

(2)、 $\frac{2 x + 1}{3} - \frac{10 x + 1}{6} = 1$

查看试题解析
21. 已知 $| x - 1 | + {(y + 2)}^{2} = 0$ ，求 $2 (3 x^{2} y - x y^{2}) - (x y^{2} + 6 x^{2} y) + 1$ 的值．

查看试题解析

22. 食品厂从生产的袋装食品中抽出样品

20

袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负来表示，记录如下表；

与标准质量的差值（单位：克）	$- 5$	$- 2$	$0$	$1$	$3$	$6$
袋数	$1$	$4$	$3$	$4$	$5$	$3$

(1)、这批样品的平均质量比标准质量是超过还是不足？平均每袋超过或不足多少克？

(2)、若每袋标准质量为

450

克，求抽样检测的样品总质量是多少？

查看试题解析

23. 如图，点 $C$ 、 $D$ 在线段 $A B$ 上， $D$ 是线段 $A B$ 中点， $A C = \frac{1}{3} A D$ ， $C D = 4$ ，求线段 $A B$ 的长．

查看试题解析
24. 某工程，甲单独做需 $12$ 天完成，乙单独做需 $8$ 天完成，现由甲先做 $2$ 天，乙再加入合作，直至完成这项工程，求完成这项工程甲共做了几天．

查看试题解析

25. 为了鼓励居民节约用水，某市自来水公司按如下方式对每户月用水量进行计算：当用水量不超过

10

方时，每方的收费标准为

a

元，当用水量超过

10

方时，超出

10

方的部分每方的收费标准为

b

元，下表是小明家

1 - 4

月份用水量和交费情况：

月份	$1$	$2$	$3$	$4$
用水量（方）	$8$	$10$	$12$	$15$
费用（元）	$16$	$20$	$26$	$35$

请根据表格中提供的信息，回答以下问题：

(1)、

a =

．

b =

；

(2)、若小明家

6

月份交纳水费

29

元，则小明家

6

月份用水多少方？

查看试题解析

26. 如图1，点 $O$ 为直线 $A B$ 上一点，过点 $O$ 作射线 $O C$ ，使 $∠ B O C = 120 °$ 将一直角三角板的直角顶点放在点 $O$ 处，一边 $O M$ 在射线 $O B$ 上，另一边 $O N$ 在直线 $A B$ 的下方．

(1)、将图1中的三角板绕点 $O$ 按每秒 $10 °$ 的速度沿顺时针方向旋转，使 $O N$ 落在 $O C$ 上．在旋转的过程中，假如第 $t$ 秒时， $O A$ 、 $O C$ 、 $O N$ 三条射线构成的角中有两个角相等，求此时 $t$ 的值为多少？

(2)、将图1中的三角板绕点 $O$ 顺时针旋转（如图2），使 $O N$ 在 $∠ A O C$ 的内部，请探究： $∠ A O M$ 与 $∠ N O C$ 之间的数量关系，并说明理由．

查看试题解析