山西省晋中市寿阳县2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2020-12-07 类型:期中考试
一、单选题
-
1. 的绝对值是( )A、3 B、 C、 D、2. 有理数 , , ,0, 中,负数的个数有A、2个 B、3个 C、4个 D、5个3. 下列错误的是( )A、2x2 -3xy-1是二次三项式 B、-x+1不是单项式 C、-22 xab2 的次数是6 D、 的系数是4. 我县10月27日至31日天气预报的最高气温与最低气温如图所示,其中温差最大的一天是( )
 A、10月28日 B、10月29日 C、10月30日 D、10月31日5. 2019年4月15日,全市“建美好家园、创魅力城市”提档升级攻坚行动动员会后,寿阳县按照市委、市政府战略部署,立即行动,一年多时间,寿阳县累计投资46.8亿元,实施路网畅通、雨污分流、大气质量、生态宜居、公共服务、城市文明、停车配套、城市品质八大提升工程,铺开83项城市建设项目,一幅大美寿阳城的蓝图正日益清晰地呈现在市民面前.数据46.8亿用科学记数法表示为( )A、 B、 C、 D、6. 某商店举办促销活动,促销的方法是将原价 元的衣服以 元出售,则下列说法中,能符合题意表达该商店促销方法的是( )A、原价减去 元后再打 折 B、原价打 折后再减去 元 C、原价减去 元后再打 折 D、原价打 折后再减去 元7. 某轮船顺水航行3h,逆水航行1.5h,已知轮船在静水中速度是x km/h,水流速度是y km/h,用式子表示轮船共航行的路程( )A、 B、 C、 D、8. 如图的正方体盒子的外表面上画有3条黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
A、10月28日 B、10月29日 C、10月30日 D、10月31日5. 2019年4月15日,全市“建美好家园、创魅力城市”提档升级攻坚行动动员会后,寿阳县按照市委、市政府战略部署,立即行动,一年多时间,寿阳县累计投资46.8亿元,实施路网畅通、雨污分流、大气质量、生态宜居、公共服务、城市文明、停车配套、城市品质八大提升工程,铺开83项城市建设项目,一幅大美寿阳城的蓝图正日益清晰地呈现在市民面前.数据46.8亿用科学记数法表示为( )A、 B、 C、 D、6. 某商店举办促销活动,促销的方法是将原价 元的衣服以 元出售,则下列说法中,能符合题意表达该商店促销方法的是( )A、原价减去 元后再打 折 B、原价打 折后再减去 元 C、原价减去 元后再打 折 D、原价打 折后再减去 元7. 某轮船顺水航行3h,逆水航行1.5h,已知轮船在静水中速度是x km/h,水流速度是y km/h,用式子表示轮船共航行的路程( )A、 B、 C、 D、8. 如图的正方体盒子的外表面上画有3条黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )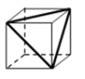 A、
A、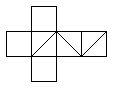 B、
B、 C、
C、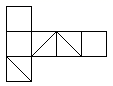 D、
D、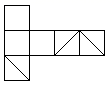 9. 已知a,b是有理数,若a在数轴上的对应点的位置如图所示,且a+b<0,有以下结论:①b<0;②b-a>0;③|-a|>-b;④ <-1.则正确的结论是( )
9. 已知a,b是有理数,若a在数轴上的对应点的位置如图所示,且a+b<0,有以下结论:①b<0;②b-a>0;③|-a|>-b;④ <-1.则正确的结论是( ) A、①④ B、①③ C、②③ D、②④10. 一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,被截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( )
A、①④ B、①③ C、②③ D、②④10. 一个纸环链,纸环按红黄绿蓝紫的顺序重复排列,被截去其中的一部分,剩下部分如图所示,则被截去部分纸环的个数可能是( ) A、2020 B、2019 C、2018 D、2017
A、2020 B、2019 C、2018 D、2017二、填空题
-
11. 比较大小: (横线上填“ ”、“ ”)12. 已知代数式 与 是同类项,则2m+3n=;13. 巴黎与北京的时差为-7小时,李阳在北京乘坐早晨6点的航班飞行10小时到达巴黎,那么李阳到达时,巴黎时间是点;14. 规定一种运算: ;计算 的值是;15. 给定一列按规律排列的数: ,1, , ,…,根据前4个数的规律,第2020个数是.
三、解答题
-
16. 计算(1)、(2)、(3)、(4)、17. 化简:(1)、(2)、18. 先化简,再求值: ,其中 .19. 小明、小兵、小英三人的家和学校在同一条东西走向的大街上,星期天班主任到这三位学生家进行家访,班主任从学校出发先向东走0.5千米到小明家,后又向东走1.5千米到小兵家,再向西走5千米到小英家,最后回到学校。(1)、以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小英三人家的位置。(2)、小明家距离小英家多远?(3)、这次家访,班主任共走了多少千米路程?20. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
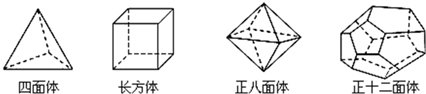 (1)、根据上面多面体模型,完成表格中的空格:
(1)、根据上面多面体模型,完成表格中的空格:多面体
顶点数(V)
面数(F)
棱数(E)
四面体
4
4
长方体
8
6
12
正八面体
8
12
正十二面体
20
12
30
(2)、你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .(3)、一个多面体的面数与顶点数相同,且有12条棱,则这个多面体的面数是 .21. 如图1,在平整的地面上,用 个棱长都为 的小正方体堆成一个几何体.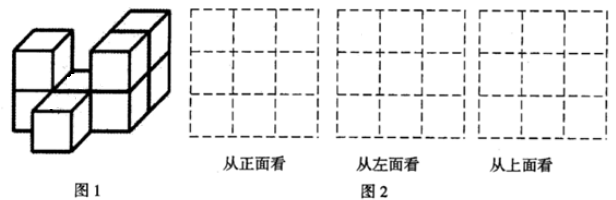 (1)、请在图2中画出从正面、左面和上面看到的这个几何体的形状图;(2)、如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加多少个小正方体;(3)、求图1中 个小正方体搭成的几何体的表面积(包括与地面接触的部分).22. 发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一
(1)、请在图2中画出从正面、左面和上面看到的这个几何体的形状图;(2)、如果现在你还有一些大小相同的小正方体,要求保持从上面和左面看到的形状图都不变,最多可以再添加多少个小正方体;(3)、求图1中 个小正方体搭成的几何体的表面积(包括与地面接触的部分).22. 发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一例1.计算: .
方法:32头尾拉开,中间相加,即3+2=5,满十进一,计算结果为352.
例2.计算:
方法:57头尾拉开,中间相加,即5+7=12,满十进一,计算结果为627
(1)、尝试:① .
② .
③ .
(2)、探究:一个两位数,十位上的数字是m,个位上的数字是n,这个两位数乘11.①若 ,计算结果的百位、十位、个位上的数字分别是什么?请通过计算加以证明
②若 ,直接写出计算结果中十位上的数字.
23. 综合实践问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
(1)、若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?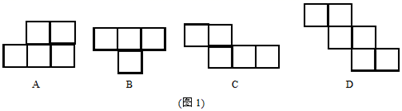 (2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
(2)、如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?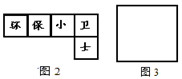 (3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
(3)、如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高以及底面积,当小正方形边长为4cm时,求纸盒的容积.