浙江省宁波十校2020-2021学年高三上学期数学期中联考试卷

试卷更新日期：2020-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x > 2}$ ， $B = {x | 0 < x < 5, x \in Z}$ ，则 $(∁_{R} A) \cap B =$ （）

A、 ${1, 2, 3, 4}$ B、 ${1, 2, 3}$ C、 ${1, 2}$ D、 ${1}$

查看试题解析
2. 若复数 $(1 + a i) (3 - i)$ （ $i$ 为虚数单位）的实部和虚部互为相反数，则实数 $a =$ （）

A、-1 B、 $- \frac{1}{2}$ C、 $\frac{1}{3}$ D、1

查看试题解析
3. 若实数 $x$ ， $y$ 满足约束条件 ${\begin{array}{l} x + y - 5 \leq 0 \\ y - 2 \geq 0 \\ x - 1 \geq 0 \end{array}$ ，则 $z = x + 2 y$ 的最大值是（）

A、5 B、7 C、9 D、11

查看试题解析
4. 某几何体的三视图如图所示（单位： $c m$ ），则该几何体的体积（单位： $c m^{3}$ ）是（）

A、 $\frac{2 π + 1}{3}$ B、 $\frac{2 π + 3}{3}$ C、 $\frac{3 π + 2}{6}$ D、 $\frac{3 π + 4}{6}$

查看试题解析
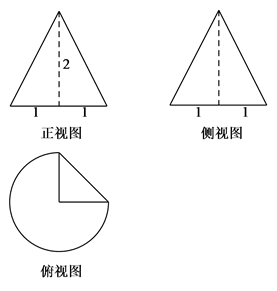5. 已知 $\vec{a} = (3, m)$ ， $\vec{b} = (2 m + 1, 1)$ ，则“ $m = 1$ ”是“ $\vec{a} // \vec{b}$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
6. 函数 $f (x) = \frac{e^{x} - e^{- x}}{\ln | x |}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
7. 如图，已知点 $E$ 、 $F$ 、G、 $H$ 分别是正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中棱 $A A_{1}$ 、 $A B$ 、 $B C$ 、 $C_{1} D_{1}$ 的中点，记二面角 $E - F G - D$ 的平面角为 $α$ ，直线 $H G$ 与平面 $A B C D$ 所成角为 $β$ ，直线 $H G$ 与直线 $D G$ 所成角为 $γ$ ，则（）

A、 $α > β > γ$ B、 $β > α > γ$ C、 $β = α > γ$ D、 $γ > α = β$

查看试题解析
8. 如图，设 $F_{1}$ 、 $F_{2}$ 分别是椭圆的左、右焦点，点 $P$ 是以 $F_{1} F_{2}$ 为直径的圆与椭圆在第一象限内的一个交点，延长 $P F_{2}$ 与椭圆交于点 $Q$ ，若 $| P F_{1} | = 4 | Q F_{2} |$ ，则直线 $P F_{2}$ 的斜率为（）

A、-2 B、-1 C、 $- \frac{1}{2}$ D、1

查看试题解析
9. 已知 $a$ ， $b \in R$ ，对任意的实数 $x$ 均有 $(| x | + a) (| x | - b) (| x | - a^{2} - 1) \geq 0$ ，则 $a + 2 b$ 的最小值为（）

A、 $\frac{15}{8}$ B、1 C、 $\frac{7}{8}$ D、2

查看试题解析
10. 已知 $\vec{e_{1}}, \vec{e_{2}}$ 为单位向量，且 $| \vec{e_{1}} + 2 \vec{e_{2}} | \leq 2$ ，若非零向量 $\vec{a}$ 满足 $\vec{a} \cdot \vec{e_{1}} \leq \vec{a} \cdot \vec{e_{2}}$ ，则 $\frac{\vec{a} \cdot (2 \vec{e_{1}} + \vec{e_{2}})}{| \vec{a} |}$ 的最大值是（）

A、 $\frac{3 \sqrt{3}}{4}$ B、 $\frac{3 \sqrt{3}}{2}$ C、 $\frac{3 \sqrt{6}}{2}$ D、 $\frac{3 \sqrt{6}}{4}$

查看试题解析

二、双空题

11. 物理中把简谐运动的图象叫做“正弦曲线”或“余弦曲线”．现有“简谐运动的图象”所对应的函数解析式是 $y = 3 \sin (\frac{1}{2} x + \frac{π}{6})$ ， $(x \in [0 ， + \infty))$ ，则该简谐运动的最小正周期是，振幅是．

查看试题解析
12. 在二项式 ${(2 x - \frac{1}{\sqrt{x}})}^{6}$ 的展开式中，常数项是，所有项的系数和为．

查看试题解析
13. 古有女子善织布，初日织三尺，日增等尺，第四日织九尺，则第七日织尺，八日共织尺．

查看试题解析
14. 一个盒子里有 $6$ 个相同的球，其中 $3$ 个红球， $2$ 个黄球， $1$ 个绿球，每次从盒中随机取出一个且不放回，则红球首先被全部取完的概率为；若红球全部被取出视为取球结束，记在此过程中取到黄球的个数为 $ξ$ ，则 $E (ξ) =$ ．

查看试题解析

三、填空题

15. 已知函数 $f (x) = e^{x} + a x^{2} + 2 a$ ，若不等式 $f (x) \geq a x (x + 1)$ 对任意 $x \in [2 ， 5]$ 恒成立，则实数a的取值范围是．

查看试题解析
16. 已知 $a > 0$ ， $b > - 2$ ，且 $a + b = 2$ ，则 $\frac{a^{2} + 4}{a} + \frac{b^{2}}{b + 2}$ 的最小值为．

查看试题解析
17. 已知圆 $C$ ： ${(x - 3)}^{2} + y^{2} = 4$ ，线段 $M N$ 在直线 $y = - 2 x + 11$ 上运动，点 $P$ 是线段 $M N$ 上任意一点，若圆 $C$ 上存在两点 $A$ ， $B$ ，使得 $P A ⊥ P B$ ，则线段 $M N$ 长度的最大值是．

查看试题解析

四、解答题

18. 在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ．已知 $(a - b + c) (\sin A + \sin B + \sin C) = (2 + \sqrt{3}) c \sin A$

(1)、求角 $B$ 的大小；

(2)、若 $b = 2$ ，求 $A C$ 边上的高的最大值．

查看试题解析
19. 如图，在四棱锥 $E - A B C D$ 中， $D C // A B$ ， $∠ B A E = ∠ B A D = 90 °$ ， $A B = A D = A E = E D = \frac{1}{2} D C$ ， $M$ 为 $E B$ 的中点．

(1)、求证： $D M ⊥ A E$ ；

(2)、求直线 $D M$ 与平面 $B C E$ 所成角的正弦值．

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且满足 $S_{n} = 2 a_{n} - 1$ $(n \in Ν^{*})$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求证 $\frac{a_{3}}{S_{2}^{2}} + \frac{a_{4}}{S_{3}^{2}} + \cdot \cdot \cdot + \frac{a_{n + 2}}{S_{n + 1}^{2}} < 2$ ， $n \in Ν^{*}$ ．

查看试题解析
21. 已知抛物线 $C_{1} : y^{2} = 2 p x (p > 0)$ ，圆 $C_{2} : {(x - 4)}^{2} + y^{2} = 4$ ．抛物线 $C_{1}$ 的焦点到其准线的距离恰好是圆 $C_{2}$ 的半径．

(1)、求抛物线 $C_{1}$ 的方程及其焦点坐标；

(2)、过抛物线 $C_{1}$ 上一点 $Q$ （除原点外）作抛物线 $C_{1}$ 的切线，交 $y$ 轴于点 $P$ ．过点 $Q$ 作圆 $C_{2}$ 的两条切线，切点分别为 $M$ 、 $N$ ．若 $M N // P Q$ ，求 $△ P M N$ 的面积．

查看试题解析
22. 已知函数 $f (x) = \frac{e^{x}}{x} - \ln x + x - 2 a$ ， $a \in R$ ．

(1)、求函数 $f (x)$ 的单调区间；

(2)、若函数 $f (x)$ 有两个不同的零点 $x_{1}$ ， $x_{2}$ ，
（i）求 $a$ 的取值范围；

（ii）证明： $| x_{2} - x_{1} | < \frac{4 a^{2} - 2 a - 1}{2 a - 1}$ ．

查看试题解析