吉林市普通高中2021届高三上学期理数第一次调研测试（期中)试卷

试卷更新日期：2020-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - x - 6 > 0}$ ， $B = {x | x \in N}$ ，则 $(∁_{R} A) \cap B$ （）

A、 ${1, 2}$ B、 ${0, 1, 2}$ C、 ${1, 2, 3}$ D、 ${0, 1, 2, 3}$

查看试题解析
2. 下列函数中最小正周期为 $π$ 的函数的个数（）
① $y = | \sin x |$ ；② $y = \cos (2 x + \frac{π}{3})$ ；③ $y = \tan 2 x$

A、0 B、1 C、2 D、3

查看试题解析
3. 下列向量中不是单位向量的是（）

A、 $(1, 0)$ B、 $(1, 1)$ C、 $(\cos α, \sin α)$ D、 $\frac{\vec{a}}{| \vec{a} |} (| \vec{a} | \neq 0)$

查看试题解析
4. 为了得到函数 $y = \cos (\frac{1}{2} x + \frac{π}{4})$ 的图象，可将函数 $y = \cos \frac{1}{2} x$ 的图象（）

A、向左平移 $\frac{π}{4}$ 个单位 B、向右平移 $\frac{π}{4}$ 个单位 C、向左平移 $\frac{π}{2}$ 个单位 D、向右平移 $\frac{π}{2}$ 个单位

查看试题解析
5. 设角 $α$ 的始边为 $x$ 轴非负半轴，则“角 $α$ 的终边在第二、三象限”是“ $\cos α < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 等差数列 ${a_{n}}$ 中， $a_{5} + a_{10} + a_{15} = 30$ ，则 $a_{22} - 2 a_{16}$ 的值为（）

A、-10 B、-20 C、10 D、20

查看试题解析
7. 已知定义在实数集 $R$ 上的偶函数 $f (x)$ 在区间 $[0, + \infty)$ 是单调增函数，若 $f (1 - a) < f (2)$ ，则实数 $a$ 的取值范围是（）

A、 $- 1 < a < 3$ B、 $a < - 1$ 或 $a > 3$ C、 $- 3 < a < 1$ D、 $a < - 3$ 或 $a > 1$

查看试题解析
8. 《周髀算经》中给出了弦图，所谓弦图（如图）是由四个全等的直角三角形和中间一个小正方形拼成一个大的正方形，若图中直角三角形两锐角分别为 $α$ ， $β$ ，且小正方形与大正方形面积之比为 $1 ： 25$ ，则 $\cos (α - β)$ 的值为（）

A、 $\frac{24}{25}$ B、1 C、 $\frac{7}{25}$ D、0

查看试题解析
9. 已知某函数的图象如图所示，则该函数的解析式可能是（）

A、 $y = (\frac{e^{x} - 1}{e^{x} + 1}) \cos x$ B、 $y = 2^{| x |} - x^{2} - 2$ C、 $y = 2^{| x |} - | x | + 2$ D、 $y = (x^{2} - 1) \cos x$

查看试题解析
10. 某兴趣小组对函数 $f (x)$ 的性质进行研究，发现函数 $f (x)$ 是偶函数，在定义域 $R$ 上满足 $f (x + 1) = f (x - 1) + f (1)$ ，且在区间 $[- 1, 0]$ 为减函数.则 $f (- 3)$ 与 $f (- \frac{5}{2})$ 的关系为（）

A、 $f (- 3) \geq f (- \frac{5}{2})$ B、 $f (- 3) > f (- \frac{5}{2})$ C、 $f (- 3) \leq f (- \frac{5}{2})$ D、 $f (- 3) < f (- \frac{5}{2})$

查看试题解析
11. 设 $I$ 为 $Δ A B C$ 的内心，延长线段 $A I$ 交线段 $B C$ 于点 $D$ ，若 $\vec{C D} = 3 \vec{D B}$ ，则 $\sin B ： \sin C =$ （）

A、2：1 B、3：1 C、4：1 D、9：1

查看试题解析
12. 已知函数 $f (x) = {\begin{matrix} \ln x ， & x \geq 1 \\ x e^{x} ， & x < 1 \end{matrix} ， g (x) = k x + f^{'} (2)$ ，对 $\forall x_{1} \in R ， \exists x_{2} \in [- 3 ， 3]$ ，使得 $f (x_{1}) \geq g (x_{2})$ 成立，则 $k$ 的取值范围是（）

A、 $(- \infty ， - \frac{1}{3 e} - \frac{1}{6}]$ B、 $[\frac{1}{3 e} + \frac{1}{6} ， + \infty)$ C、 $[- \frac{1}{3 e} - \frac{1}{6} ， \frac{1}{3 e} + \frac{1}{6}]$ D、 $(- \infty ， - \frac{1}{3 e} - \frac{1}{6}]$ $\cup$ $[\frac{1}{3 e} + \frac{1}{6} ， + \infty)$

查看试题解析

二、填空题

13. 已知复数 $z = 2 - 3 i$ ，则 $| z + 1 | =$ .

查看试题解析
14. 已知函数 $f (x) = a^{1 - x}$ $(a > 0$ 且 $a \neq 1)$ ，若 $f (2021) > f (2020)$ ，则实数 $a$ 的取值范围是.

查看试题解析
15. 有一个数阵排列如下：
1   2   4   7   11 16 22……

3   5   8   12 17 23…………

6   9   13 18 24………………

10 14 19 25……………………

15 20 26…………………………

21 27………………………………

28……………………………………

………………………………………

则第40行从左至右第6个数字为.

查看试题解析
16. 如图所示，滨江公园内有一块三角形形状的草坪 $A B C$ ，经测量得 $A B = 30 m ， A C = 40 m ， B C = 10 \sqrt{13} m$ ，在保护草坪的同时，为了方便游人行走，现打算铺设一条小路 $D E$ （其中点 $D$ 在边 $A B$ 上，点 $E$ 在边 $A C$ 上），若 $D E$ 恰好将该草坪的面积平分，则 $D ， E$ 两点间的最小距离为 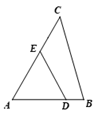$m$ .

查看试题解析

三、解答题

17. 数列 ${b_{n}}$ 前 $n$ 项和为 $S_{n}$ 且 $b_{1} = 1, b_{n + 1} = \frac{1}{2} S_{n}$ ，

(1)、求 ${b_{n}}$ 的通项公式；

(2)、求 $b_{2} + b_{4} + b_{6} + \dots + b_{2 n}$ 值.

查看试题解析
18. 已知函数 $f (x) = 2 \sin x \cos (x - \frac{π}{3})$ ， $x \in R$ ，

(1)、求函数 $f (x)$ 的对称中心；

(2)、若存在 $x_{0} \in [\frac{π}{4} ， \frac{3 π}{4}]$ ，使不等式 $f (x_{0}) < m$ 成立，求实数 $m$ 的取值范围.

查看试题解析
19. 在 $△ A B C$ 中， $a, b, c$ 分别是内角 $A, B, C$ 的对边， $\sqrt{3} a = c \sin B + \sqrt{3} b \cos C$ ，

(1)、求角 $B$ 的大小；

(2)、若 $b = 4$ ，且 $△ A B C$ 的面积等于 $4 \sqrt{3}$ ，求 $a, c$ 的值.

查看试题解析
20. 已知函数 $f (x) = \frac{1}{3} a x^{3} + \frac{2 a + 1}{2} x^{2} + 3 x$ ，

(1)、当 $a = 2$ 时，求函数 $f (x)$ 的单调区间与极值；

(2)、是否存在正实数 $a$ ，使得函数 $f (x)$ 在区间 $[- 1 ， 1]$ 上为减函数？若存在，请求 $a$ 的取值范围；若不存在，请说明理由.

查看试题解析
21. 已知数列 ${a_{n}}$ 的首项 $a_{1} = 3$ ，且满足 $a_{n + 1} = 2 a_{n} + 2^{n + 1} - 1$ .

(1)、设 $b_{n} = \frac{a_{n} - 1}{2^{n}}$ ，证明 ${b_{n}}$ 是等差数列；

(2)、求数列 ${a_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
22. 设函数 $f (x) = m \ln x - 2 x$ ，

(1)、当 $m = 2$ 时，求函数 $f (x)$ 在点 $(1 ， f (1))$ 处的切线；

(2)、若 $\forall x > 0$ ，都有 $f (x) \leq 0$ ，求正实数 $m$ 的取值范围；

(3)、当 $m = 1$ 时，曲线 $y = f (x)$ 上的点 $(x_{0} ， y_{0}) (x_{0} > 0)$ 处的切线与 $y = x^{2}$ 相切，求满足条件的 $x_{0}$ 的个数.

查看试题解析