山东省枣庄市山亭区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
1. 如图,在平行四边形 中, 、 是 上两点, ,连接 、 、 、 ,添加一个条件,使四边形 是矩形,这个条件是( )
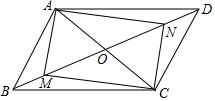 A、 B、 C、 D、2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 一个菱形的边长是方程 的一个根,其中一条对角线长为8,则该菱形的面积为( )A、48 B、24 C、24或40 D、48或804. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )
A、 B、 C、 D、2. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根3. 一个菱形的边长是方程 的一个根,其中一条对角线长为8,则该菱形的面积为( )A、48 B、24 C、24或40 D、48或804. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )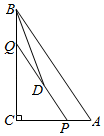 A、 B、 C、 D、5. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
A、 B、 C、 D、5. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、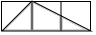 B、
B、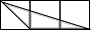 C、
C、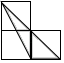 D、
D、 6. 某个几何体的三视图如图所示,该几何体是( )
6. 某个几何体的三视图如图所示,该几何体是( ) A、
A、 B、
B、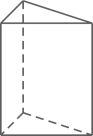 C、
C、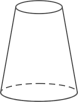 D、
D、 7. 若点 , , 在反比例函数 的图像上,则 的大小关系是( )A、 B、 C、 D、8. 如图,在 中, ,则 sinB 的值为( )
7. 若点 , , 在反比例函数 的图像上,则 的大小关系是( )A、 B、 C、 D、8. 如图,在 中, ,则 sinB 的值为( ) A、 B、 C、 D、9. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )
A、 B、 C、 D、9. 如图,在 的正方形网格中,每个小正方形的边长都是 , 的顶点都在这些小正方形的顶点上,则 的值为( )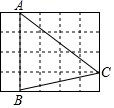 A、 B、 C、 D、10. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为( )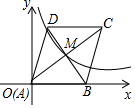 A、 B、 C、2 D、11. 把函数 的图象,经过怎样的平移变换以后,可以得到函数 的图象( )A、向左平移 个单位,再向下平移 个单位 B、向左平移 个单位,再向上平移 个单位 C、向右平移 个单位,再向上平移 个单位 D、向右平移 个单位,再向下平移 个单位12. 如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G,下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE= S△CEF , 其中正确的是( )
A、 B、 C、2 D、11. 把函数 的图象,经过怎样的平移变换以后,可以得到函数 的图象( )A、向左平移 个单位,再向下平移 个单位 B、向左平移 个单位,再向上平移 个单位 C、向右平移 个单位,再向上平移 个单位 D、向右平移 个单位,再向下平移 个单位12. 如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点G,下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF=60°时,S△ABE= S△CEF , 其中正确的是( ) A、①③ B、②④ C、①③④ D、②③④
A、①③ B、②④ C、①③④ D、②③④二、填空题
-
13. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.14. 一个圆柱的三视图如图所示,若其俯视图为圆,则这个圆柱的体积为 .
 15. 如图,在矩形 中, ,对角线 与 相交于点 , ,垂足为点 ,且 平分 ,则 的长为.
15. 如图,在矩形 中, ,对角线 与 相交于点 , ,垂足为点 ,且 平分 ,则 的长为.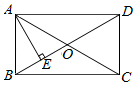 16. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O , 且 ,则 .
16. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O , 且 ,则 . 17. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .18. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
17. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .18. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)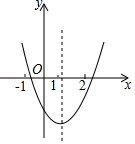
三、解答题
-
19. 已知关于x的方程 有实数根.(1)、求 的取值范围;(2)、若该方程有两个实数根,分别为 和 ,当 时,求 的值.20. 为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等(1)、若从中只录用一人,恰好选到思政专业毕业生的概率是:(2)、若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.21. 如图,在正方形 中,点 是 的中点,连接 ,过点 作 交 于点 ,交 于点 .
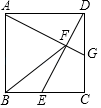 (1)、证明: ;(2)、连接 ,证明: .22. 某体育看台侧面的示意图如图所示,观众区 的坡度为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .求:
(1)、证明: ;(2)、连接 ,证明: .22. 某体育看台侧面的示意图如图所示,观众区 的坡度为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .求: (1)、观众区的水平宽度 ;(2)、顶棚的 处离地面的高度 .( , ,结果精确到 )23. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .
(1)、观众区的水平宽度 ;(2)、顶棚的 处离地面的高度 .( , ,结果精确到 )23. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .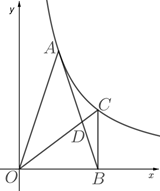 (1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.24. 当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.(1)、直接写出书店销售该科幻小说时每天的销售量 (本)与销售单价 (元)之间的函数关系式及自变量的取值范围.(2)、书店决定每销售1本该科幻小说,就捐赠 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 的值.25. 已知:如图,抛物线 与坐标轴分别交于点 , 点 是线段 上方抛物线上的一个动点,
(1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.24. 当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.(1)、直接写出书店销售该科幻小说时每天的销售量 (本)与销售单价 (元)之间的函数关系式及自变量的取值范围.(2)、书店决定每销售1本该科幻小说,就捐赠 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求 的值.25. 已知:如图,抛物线 与坐标轴分别交于点 , 点 是线段 上方抛物线上的一个动点, (1)、求抛物线解析式:(2)、当点 运动到什么位置时, 的面积最大?
(1)、求抛物线解析式:(2)、当点 运动到什么位置时, 的面积最大?