山东省泰安市新泰市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四个几何体中，左视图是四边形的几何体共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 对于反比例函数y＝﹣ $\frac{3}{x}$ ，下列说法正确的有（）
①图象经过点（1，﹣3）；②图象分布在第二、四象限；③当x＞0时，y随x的增大而增大；④点A（x₁ ， y₁）、B（x₂ ， y₂）都在反比例函数y＝﹣ $\frac{3}{x}$ 的图象上，若x₁＜x₂ ，则y₁＜y₂ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，已知一次函数y＝ax+b与反比例函数y＝ $\frac{k}{x}$ 图象交于M、N两点，则不等式ax+b＞ $\frac{k}{x}$ 解集为（）

A、x＞2或﹣1＜x＜0 B、﹣1＜x＜0 C、﹣1＜x＜0或0＜x＜2 D、x＞2

查看试题解析
4. 在Rt△ABC中，∠C＝90°，AB＝10，sin∠B＝ $\frac{3}{5}$ ，则BC＝（）

A、15 B、6 C、9 D、8

查看试题解析
5. 一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球，随机从中摸出一球，不再放回袋中，充分搅匀后再随机摸出一球．两次都摸到红球的概率是（）

A、 $\frac{3}{10}$ B、 $\frac{9}{25}$ C、 $\frac{9}{20}$ D、 $\frac{3}{5}$

查看试题解析
6. 若 $A (- 4 ， y_{1})$ ， $B (- \frac{1}{4} ， y_{2})$ ， $C (3 ， y_{3})$ 为二次函数 $y = {(x + 2)}^{2} - 9$ 的图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、y₁<y₂<y₃ B、y₂<y₁<y₃ C、y₃<y₁<y₂ D、y₁<y₃<y₂

查看试题解析
7. 如图，点A，B，C，在⊙O上，∠ABO=32°，∠ACO=38°，则∠BOC等于（）

A、60° B、70° C、120° D、140°

查看试题解析
8. 对于抛物线 $y = x^{2} - 2 x - 1$ ，下列说法中错误的是（）

A、顶点坐标为 $(1, - 2)$ B、对称轴是直线 $x = 1$ C、当 $x > 1$ 时， $y$ 随 $x$ 的增大减小 D、抛物线开口向上

查看试题解析
9. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，下列式子正确的是（）

A、sinA＝ $\frac{BD}{BC}$ B、cosA＝ $\frac{AC}{AD}$ C、tanA＝ $\frac{CD}{AB}$ D、cosB＝ $\frac{AC}{AB}$

查看试题解析
10. 如图，⊙O是△ABC的外接圆，∠B=60°，OP⊥AC于点P，OP=2 $\sqrt{3}$ ，则⊙O的半径为（）．

A、4 $\sqrt{3}$ B、6 $\sqrt{3}$ C、8 D、12

查看试题解析
11. 如图，某厂生产一种扇形折扇，OB=10cm，AB=20cm，其中裱花的部分是用纸糊的，若扇子完全打开摊平时纸面面积为 $\frac{1000}{3}$ π cm² ，则扇形圆心角的度数为（）

A、120° B、140° C、150° D、160°

查看试题解析
12. 抛物线y=ax²+bx+c的对称轴为直线x=﹣1，部分图象如图所示，下列判断中：
①abc＞0；②b²﹣4ac＞0；③9a﹣3b+c=0；④若点（﹣0.5，y₁），（﹣2，y₂）均在抛物线上，则y₁＞y₂；⑤5a﹣2b+c＜0．其中正确的个数有（）

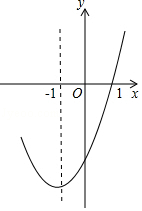A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 如图， $\overset{⌢}{A B}$ 是半圆，点O为圆心，C、D两点在 $\overset{⌢}{A B}$ 上，且AD∥OC，连接BC、BD．若 $\overset{⌢}{C D}$ ＝65°，则∠ABD的度数为．

查看试题解析
14.
如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进20海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海岛C到航线AB的距离CD等于海里．

查看试题解析
15. 如图，平行四边形ABCD的一边AB在x轴上，长为5，且∠DAB＝60°，反比例函数y＝ $\frac{2 \sqrt{3}}{x}$ 和y＝ $- \frac{3 \sqrt{3}}{x}$ 分别经过点C，D，则AD＝．

查看试题解析
16. 有三张正面分别写有数字﹣1，1，2的卡片，它们背面完全相同，现将这三张卡片背面朝上洗匀后随即抽取一张，以其正面数字作为a的值，然后再从剩余的两张卡片随机抽一张，以其正面的数字作为b的值，则点（a，b）在第二象限的概率为．

查看试题解析
17. 《孙子算经》是我国古代重要的数学著作，成书于约一千五百年前，其中有道歌谣算题：“今有竿不知其长，量得影长一丈五尺，立一标杆，长一尺五寸，影长五寸，问杆长几何？”歌谣的意思是：有一根竹竿不知道有多长，量出它在太阳下的影子长一丈五，同时立一根一尺五的小标杆，它的影长五寸（提示：仗和尺是古代的长度单位，1丈＝10尺，1尺＝10寸），可以求出竹竿的长为尺．

查看试题解析
18. 如图是某几何体的三视图及相关数据，则该几何体的侧面积是．

查看试题解析

三、解答题

19. 计算题：

(1)、计算： $\sqrt{2}$ sin45°+cos²30°•tan60°﹣tan45°；

(2)、已知是锐角， $2 \sin (a - 15 °) = \sqrt{2}$ ，求 $\frac{\sin a}{\sqrt{3}} - | \cos a - \tan \frac{a}{2} |$ ．

查看试题解析
20. 在一次数学兴趣小组活动中，阳光和乐观两位同学设计了如图所示的两个转盘做游戏（每个转盘被分成面积相等的几个扇形，并在每个扇形区域内标上数字）．游戏规则如下：两人分别同时转动甲、乙转盘，转盘停止后，若指针所指区域内两数和小于12，则阳光获胜，反之则乐观获胜（若指针停在等分线上，重转一次，直到指针指向某一份内为止）．

(1)、请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果；

(2)、游戏对双方公平吗？请说明理由．

查看试题解析
21. 如图，在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，点C坐标为（﹣1，0），点A坐标为（0，2）．一次函数y＝kx+b的图象经过点B、C，反比例函数y＝ $\frac{m}{x}$ 的图象经过点B．

(1)、求一次函数和反比例函数的关系式；

(2)、直接写出当x＜0时，kx+b﹣ $\frac{m}{x}$ ＜0的解集；

(3)、在x轴上找一点M，使得AM+BM的值最小，直接写出点M的坐标和AM+BM的最小值．

查看试题解析
22. 如图，某仓储中心有一斜坡AB，其坡比为i＝1∶2，顶部A处的高AC为4 m，B，C在同一水平面上．

(1)、求斜坡AB的水平宽度BC；

(2)、矩形DEFG为长方形货柜的侧面图，其中DE＝2.5 m，EF＝2 m．将货柜沿斜坡向上运送，当BF＝3.5 m时，求点D离地面的高．( $\sqrt{5}$ ≈2.236，结果精确到0.1 m)

查看试题解析
23. 一汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系：

x

3000

3200

3500

4000

y

100

96

90

80

(1)、观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式.

(2)、已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．用含x（x≥3000）的代数式填表:

租出的车辆数

未租出的车辆数

租出每辆车的月收益

所有未租出的车辆每月的维护费

(3)、若你是该公司的经理，你会将每辆车的月租金定为多少元，才能使公司获得最大月收益？请求出公司的最大月收益是多少元．

查看试题解析
24. 如图，AB是⊙O的直径，点C是⊙O上一点，AC平分∠DAB，直线DC与AB的延长线相交于点P，AD与PC延长线垂直，垂足为点D，CE平分∠ACB，交AB于点F，交⊙O于点E.

(1)、求证：PC与⊙O相切；

(2)、求证：PC＝PF；

(3)、若AC＝8，tan∠ABC＝ $\frac{4}{3}$ ，求线段BE的长.

查看试题解析
25. 如图，抛物线y＝﹣ $\frac{1}{2}$ x²+ $\frac{3}{2}$ x+2与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线1交抛物线于点Q．

(1)、求点A、点B、点C的坐标；

(2)、当点P在线段OB上运动时，直线1交直线BD于点M，试探究m为何值时，四边形CQMD是平行四边形；

(3)、点P在线段AB上运动过程中，是否存在点Q，使得以点B、Q、M为顶点的三角形与△BOD相似？若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析

租出的车辆数		未租出的车辆数
租出每辆车的月收益		所有未租出的车辆每月的维护费

x	3000	3200	3500	4000
y	100	96	90	80