山东省泰安市宁阳县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
1. 已知正比例函数y=kx的图象经过第二、四象限,则一次函数y=kx﹣k的图象可能是图中的( )A、
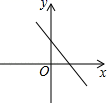 B、
B、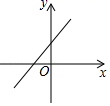 C、
C、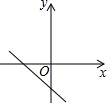 D、
D、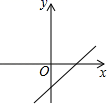 2. 已知反比例函数y=2x﹣1 , 下列结论中,错误的是( )A、点(﹣2,﹣1)在它的图象上 B、y随x的增大而减小 C、图象在第一、三象限 D、若x<0时,y随x的增大而减小3. 如图,A 、 B是曲线 上的点,经过A、 B两点向x 轴、y轴作垂线段,若S阴影=1 则 S1+S2 =( )
2. 已知反比例函数y=2x﹣1 , 下列结论中,错误的是( )A、点(﹣2,﹣1)在它的图象上 B、y随x的增大而减小 C、图象在第一、三象限 D、若x<0时,y随x的增大而减小3. 如图,A 、 B是曲线 上的点,经过A、 B两点向x 轴、y轴作垂线段,若S阴影=1 则 S1+S2 =( ) A、4 B、5 C、6 D、84. 二次函数y=2x2﹣4x﹣6的最小值是( )A、﹣8 B、﹣2 C、0 D、65. 在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在 附近,则箱中卡的总张数可能是A、1张 B、4张 C、9张 D、12张6. 如图,△ABC的三边的中线AD,BE,CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( )
A、4 B、5 C、6 D、84. 二次函数y=2x2﹣4x﹣6的最小值是( )A、﹣8 B、﹣2 C、0 D、65. 在一个不透明的箱子中有3张红卡和若干张绿卡,它们除了颜色外其他完全相同,通过多次抽卡试验后发现,抽到绿卡的概率稳定在 附近,则箱中卡的总张数可能是A、1张 B、4张 C、9张 D、12张6. 如图,△ABC的三边的中线AD,BE,CF的公共点为G,且AG:GD=2:1,若S△ABC=12,则图中阴影部分的面积是( ) A、3 B、4 C、5 D、67. 如图,AB是半圆O的直径,∠BAC=40°,则∠D的度数是( )
A、3 B、4 C、5 D、67. 如图,AB是半圆O的直径,∠BAC=40°,则∠D的度数是( ) A、140° B、130° C、120° D、110°8. 一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、2、4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之和为偶数的概率是( )A、 B、 C、 D、9. 在如图所示的网格纸中,有A、B两个格点,试取格点C , 使得△ABC是等腰三角形,则这样的格点C的个数是( )
A、140° B、130° C、120° D、110°8. 一个不透明的袋中有四张完全相同的卡片,把它们分别标上数字1、2、2、4.随机抽取一张卡片,然后放回,再随机抽取一张卡片,则两次抽取的卡片上数字之和为偶数的概率是( )A、 B、 C、 D、9. 在如图所示的网格纸中,有A、B两个格点,试取格点C , 使得△ABC是等腰三角形,则这样的格点C的个数是( ) A、4 B、6 C、8 D、1010. 如图,在△ABC中,∠BOC=140°,I是内心,O是外心,则∠BIC等于( )
A、4 B、6 C、8 D、1010. 如图,在△ABC中,∠BOC=140°,I是内心,O是外心,则∠BIC等于( ) A、130° B、125° C、120° D、115°11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )
A、130° B、125° C、120° D、115°11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0),则下面的四个结论,其中正确的个数为( )①2a+b=0②4a﹣2b+c<0③ac>0④当y>0时,﹣1<x<4
 A、1个 B、2个 C、3个 D、4个12. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A、1个 B、2个 C、3个 D、4个12. 将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )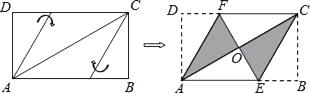 A、1 B、 C、 D、4
A、1 B、 C、 D、4二、填空题
-
13. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,若AD=3,CE=5,则CD等于 .
 14. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 .
14. 如图,在△ABC中,sinB= ,tanC= ,AB=3,则AC的长为 . 15. 圆锥的侧面展开图的圆心角是120°,其底面圆的半径为2cm , 则其侧面积为 .16. 如图,PA,PB分别切⊙O于点A,B.若∠P=100°,则∠ACB的大小为(度).
15. 圆锥的侧面展开图的圆心角是120°,其底面圆的半径为2cm , 则其侧面积为 .16. 如图,PA,PB分别切⊙O于点A,B.若∠P=100°,则∠ACB的大小为(度).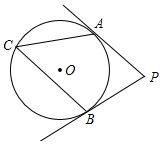 17. 如图,在 ABCD中,点E是AD边上一点,AE:ED=1:2,连接AC、BE交于点F.若S△AEF=1,则S四边形CDEF=.
17. 如图,在 ABCD中,点E是AD边上一点,AE:ED=1:2,连接AC、BE交于点F.若S△AEF=1,则S四边形CDEF=. 18. 如图,已知OP平分∠AOB , CP∥OA , PD⊥OA于点D , PE⊥OB于点E . CP= ,PD=6.如果点M是OP的中点,则DM的长是 .
18. 如图,已知OP平分∠AOB , CP∥OA , PD⊥OA于点D , PE⊥OB于点E . CP= ,PD=6.如果点M是OP的中点,则DM的长是 .
三、解答题
-
19. 如图,直线y=ax+b与x轴交于点A(4,0),与y轴交于点B(0,﹣2),与反比例函数y= (x>0)的图象交于点C(6,m).
 (1)、求直线和反比例函数的表达式;(2)、连接OC , 在x轴上找一点P , 使△OPC是以OC为腰的等腰三角形,请求出点P的坐标;(3)、结合图象,请直接写出不等式 ≥ax+b的解集.20. 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG , 过点A作AH∥DG , 交BG于点H . 连接HF , AF , 其中AF交EC于点M .
(1)、求直线和反比例函数的表达式;(2)、连接OC , 在x轴上找一点P , 使△OPC是以OC为腰的等腰三角形,请求出点P的坐标;(3)、结合图象,请直接写出不等式 ≥ax+b的解集.20. 如图,正方形ABCD的边CD在正方形ECGF的边CE上,连接DG , 过点A作AH∥DG , 交BG于点H . 连接HF , AF , 其中AF交EC于点M . (1)、求证:△AHF为等腰直角三角形.(2)、若AB=3,EC=5,求EM的长.21. 如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈ ,cos27°≈ ,tan27°≈ ,sin53°≈ ,cos53°≈ ,tan53°≈ )
(1)、求证:△AHF为等腰直角三角形.(2)、若AB=3,EC=5,求EM的长.21. 如图,海上有A、B、C三座小岛,小岛B在岛A的正北方向,距离为121海里,小岛C分别位于岛B的南偏东53°方向,位于岛A的北偏东27°方向,求小岛B和小岛C之间的距离.(参考数据:sin27°≈ ,cos27°≈ ,tan27°≈ ,sin53°≈ ,cos53°≈ ,tan53°≈ ) 22. 如图,已知△ABC中,AB=8,BC=10,AC=12,D是AC边上一点,且AB2=AD•AC,连接BD,点E、F分别是BC、AC上两点(点E不与B、C重合),∠AEF=∠C,AE与BD相交于点G.
22. 如图,已知△ABC中,AB=8,BC=10,AC=12,D是AC边上一点,且AB2=AD•AC,连接BD,点E、F分别是BC、AC上两点(点E不与B、C重合),∠AEF=∠C,AE与BD相交于点G. (1)、求BD的长;(2)、求证△BGE∽△CEF;(3)、连接FG,当△GEF是等腰三角形时,直接写出BE的所有可能的长度.23. 如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点.
(1)、求BD的长;(2)、求证△BGE∽△CEF;(3)、连接FG,当△GEF是等腰三角形时,直接写出BE的所有可能的长度.23. 如图,△OAP是等腰直角三角形,∠OAP=90°,点A在第四象限,点P坐标为(8,0),抛物线y=ax2+bx+c经过原点O和A、P两点. (1)、求抛物线的函数关系式.(2)、点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;(3)、在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.
(1)、求抛物线的函数关系式.(2)、点B是y轴正半轴上一点,连接AB,过点B作AB的垂线交抛物线于C、D两点,且BC=AB,求点B坐标;(3)、在(2)的条件下,点M是线段BC上一点,过点M作x轴的垂线交抛物线于点N,求△CBN面积的最大值.