山东省泰安市岱岳区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
1.
如图,几何体是由3个大小完全一样的正方体组成的,它的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )A、 B、 C、 D、3. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )
2. 一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )A、 B、 C、 D、3. 关于x的一元二次方程x2﹣ x+sinα=0有两个相等的实数根,则锐角α等于( )
A、15° B、30° C、45° D、60°4. 如图,点B,C,D在⊙O上,若∠BCD=30°,则∠BOD的度数是( ) A、75° B、70° C、65° D、60°5. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )
A、75° B、70° C、65° D、60°5. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D,现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )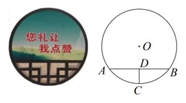 A、6dm B、5dm C、4dm D、3dm6. 如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )
A、6dm B、5dm C、4dm D、3dm6. 如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )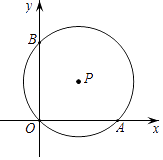 A、2 B、3 C、4 D、57. 如图,二次函数y=ax2+bx+c(a>0)的图象与x轴的交点A、B的横坐标分别为﹣1和3,则函数值y随x值的增大而减小时,x的取值范围是( )
A、2 B、3 C、4 D、57. 如图,二次函数y=ax2+bx+c(a>0)的图象与x轴的交点A、B的横坐标分别为﹣1和3,则函数值y随x值的增大而减小时,x的取值范围是( ) A、x<1 B、x>1 C、x<2 D、x>28. 已知圆锥的高为12,底面圆的半径为5,则该圆锥的侧面展开图的面积为( )A、65π B、60π C、75π D、70π9. 已知函数y=ax2+bx+c(a≠0)的图象如图,则函数y=ax+b与y= 的图象大致为( )
A、x<1 B、x>1 C、x<2 D、x>28. 已知圆锥的高为12,底面圆的半径为5,则该圆锥的侧面展开图的面积为( )A、65π B、60π C、75π D、70π9. 已知函数y=ax2+bx+c(a≠0)的图象如图,则函数y=ax+b与y= 的图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 上一点,BD交AC于点E,若BC=4,AD= ,则AE的长是( )
10. 如图,已知⊙O是等腰Rt△ABC的外接圆,点D是 上一点,BD交AC于点E,若BC=4,AD= ,则AE的长是( ) A、1 B、1.2 C、2 D、311. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点A(10,0),sin∠COA= .若反比例函数 经过点C,则k的值等于( )
A、1 B、1.2 C、2 D、311. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点A(10,0),sin∠COA= .若反比例函数 经过点C,则k的值等于( ) A、10 B、24 C、48 D、50.12. 已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A、10 B、24 C、48 D、50.12. 已知二次函数y=a(x﹣h)2+k(a>0),其图象过点A(0,2),B(8,3),则h的值可以是( )
A、6 B、5 C、4 D、3二、填空题
-
13. 二次函数y=2(x﹣3)2+4的图象的对称轴为x= .14. 在一个不透明的盒子中装有n个小球,它们只有颜色上的区别,其中有2个红球,每次摸球前先将盒中的球摇匀,随机摸出一个球记下颜色后再放回盒中,通过大量重复试验后发现,摸到红球的频率稳定于0.2,那么可以推算出n大约是 .15. 如图,已知⊙O上三点A,B,C,半径OC= ,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为 .
 16. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.
16. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为度.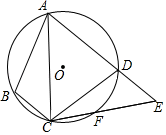 17. 如图,反比例函数y= (x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S△ACD= ,则S矩形BDOE= .
17. 如图,反比例函数y= (x>0)经过A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥y轴于点D,过点B作BE⊥x轴于点E,连接AD,已知AC=1,BE=1,S△ACD= ,则S矩形BDOE= . 18. 如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为 .
18. 如图,ABCD是平行四边形,AB是⊙O的直径,点D在⊙O上,AD=OA=2,则图中阴影部分的面积为 .
三、解答题
-
19. 某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)、请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;(2)、假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.20. 如图,一次函数 的图象与反比例函数 的图象相交于 两点,与 轴相交于点 .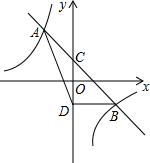 (1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.21. 如图,海中有两个小岛 , ,某渔船在海中的 处测得小岛D位于东北方向上,且相距 ,该渔船自西向东航行一段时间到达点 处,此时测得小岛 恰好在点 的正北方向上,且相距 ,又测得点 与小岛 相距 .
(1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.21. 如图,海中有两个小岛 , ,某渔船在海中的 处测得小岛D位于东北方向上,且相距 ,该渔船自西向东航行一段时间到达点 处,此时测得小岛 恰好在点 的正北方向上,且相距 ,又测得点 与小岛 相距 .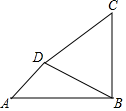 (1)、求 的值;(2)、求小岛 , 之间的距离(计算过程中的数据不取近似值).22. 如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙0与AC相切于点D,BD平分∠ABC,AD= OD,AB=12,求CD的长.
(1)、求 的值;(2)、求小岛 , 之间的距离(计算过程中的数据不取近似值).22. 如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙0与AC相切于点D,BD平分∠ABC,AD= OD,AB=12,求CD的长. 23. 已知二次函数y=x2+2mx+(m2﹣1)(m是常数).(1)、若它的图象与x轴交于两点A,B,求线段AB的长;(2)、若它的图象的顶点在直线y= x+3上,求m的值.
23. 已知二次函数y=x2+2mx+(m2﹣1)(m是常数).(1)、若它的图象与x轴交于两点A,B,求线段AB的长;(2)、若它的图象的顶点在直线y= x+3上,求m的值.