山东省日照市五莲县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
1. 如果2是方程x2-3x+k=0的一个根,则常数k的值为( ).A、2 B、1 C、-1 D、-22. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列函数中是反比例函数的是( )A、 B、 C、 D、4. 若关于 的一元二次方程 有实数根,则 的取值范围( )A、 B、 C、 且 D、 且5. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )
3. 下列函数中是反比例函数的是( )A、 B、 C、 D、4. 若关于 的一元二次方程 有实数根,则 的取值范围( )A、 B、 C、 且 D、 且5. 如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( ) A、1 B、 C、2 D、26. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )A、10m B、12m C、15m D、40m7. 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y= 的图象可能是( )
A、1 B、 C、2 D、26. 在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为( )A、10m B、12m C、15m D、40m7. 二次函数y=ax2+bx+c(a,b,c为常数且a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y= 的图象可能是( )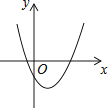 A、
A、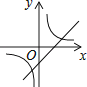 B、
B、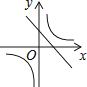 C、
C、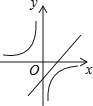 D、
D、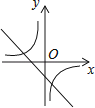 8. 如图,在平行四边形 中 : : 若 ,则 ( )
8. 如图,在平行四边形 中 : : 若 ,则 ( ) A、18 B、12 C、10 D、89. 如图, 是 的直径,点 是 延长线上一点, 是 的切线,点 是切点, ,若 半径为 ,则图中阴影部分的面积为( )
A、18 B、12 C、10 D、89. 如图, 是 的直径,点 是 延长线上一点, 是 的切线,点 是切点, ,若 半径为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、10. 如图, 中, 且 ,若点 在反比例函数 的图象上,点 在反比例函数 的图象上,则 的值为( )
A、 B、 C、 D、10. 如图, 中, 且 ,若点 在反比例函数 的图象上,点 在反比例函数 的图象上,则 的值为( ) A、 B、 C、3 D、-311. 在平面直角坐标系中,以原点 为位似中心,位似比为 : ,将 缩小,若点 坐标 , ,则点 对应点 坐标为( )A、 , B、 C、 或 , D、 , 或 ,12. 如图,抛物线 的对称轴为直线 ,与 轴的 个交点坐标为 , ,其部分图象如图所示,下列结论:① ;②方程 的两个根是 , ;③ ;④当 时, 的取值范围是 .其中结论正确的个数是( )
A、 B、 C、3 D、-311. 在平面直角坐标系中,以原点 为位似中心,位似比为 : ,将 缩小,若点 坐标 , ,则点 对应点 坐标为( )A、 , B、 C、 或 , D、 , 或 ,12. 如图,抛物线 的对称轴为直线 ,与 轴的 个交点坐标为 , ,其部分图象如图所示,下列结论:① ;②方程 的两个根是 , ;③ ;④当 时, 的取值范围是 .其中结论正确的个数是( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 一种药品原价每盒25元,两次降价后每盒16元.设两次降价的百分率都为x,可列方程.14. 用半径为6cm,圆心角为120°的扇形围成一个圆锥,则圆锥的底面圆半径为cm.15. 如图,在平面直角坐标系 中,四边形 和四边形 都是正方形,点 在 轴的正半轴上,点 在边 上,反比例函数 的图象过点 、 .若 ,则 的值为 .
 16. 如图,在直角坐标系中,已知点 , , , ,对 述续作旋转变换,依次得 、 、 、 ...,则 的直角顶点的坐标为 .
16. 如图,在直角坐标系中,已知点 , , , ,对 述续作旋转变换,依次得 、 、 、 ...,则 的直角顶点的坐标为 .
三、解答题
-
17. 用合适的方法解方程:(1)、 ;(2)、 .18. 学校决定每班选取4名同学参加12.2全国交通安全日 细节关乎生命安全文明出行 主题活动启动仪式,班主任决定从4名同学(小明、小山、小月、小玉)中通过抽签的方式确定2名同学去参加该活动.抽签规则:将4名同学的姓名分别写在4张完全相同的卡片正面,把4张卡片的背面朝上,洗匀后放在桌子上,王老师先从中随机抽取一张卡片,记下名字,再从剩余的3张卡片中随机抽取一张,记下名字.(1)、 小刚被抽中 是事件, 小明被抽中 是事件(填 不可能 、 必然 、 随机),第一次抽取卡片抽中是小玉的概率是;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出小月被抽中的概率.19. 如图,在平面直角坐标系中, 为坐标原点, 的边 垂直于 轴、垂足为点 ,反比例函数 的图象经过 的中点 、且与 相交于点 .经过 、 两点的一次函数解析式为 ,若点 的坐标为 , .且 .
 (1)、求反比例函数的解析式;(2)、在直线 上有一点 , 的面积等于 .求满足条件的点 的坐标;(3)、请观察图象直接写出不等式 的解集.20. 为支持大学生勤工俭学,市政府向某大学生提供了1万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件10元.每天还要支付其他费用25元.该产品每天的销售量 件 与销售单价 元 关系为 .(1)、设每天的利润为 元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元? 注:每天的利润 每天的销售利润一每天的支出费用(2)、若销售单价不得低于其生产成本,且销售每件产品的利润率不能超过50%,则该学生最快用多少天可以还清无息贷款?
(1)、求反比例函数的解析式;(2)、在直线 上有一点 , 的面积等于 .求满足条件的点 的坐标;(3)、请观察图象直接写出不等式 的解集.20. 为支持大学生勤工俭学,市政府向某大学生提供了1万元的无息贷款用于销售某种自主研发的产品,并约定该学生用经营的利润逐步偿还无息贷款,已知该产品的生产成本为每件10元.每天还要支付其他费用25元.该产品每天的销售量 件 与销售单价 元 关系为 .(1)、设每天的利润为 元,当销售单价定为多少元时,每天的利润最大?最大利润为多少元? 注:每天的利润 每天的销售利润一每天的支出费用(2)、若销售单价不得低于其生产成本,且销售每件产品的利润率不能超过50%,则该学生最快用多少天可以还清无息贷款?

