山东省济宁市微山县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列式子中表示 $y$ 是关于 $x$ 的反比例函数的是（）

A、 $y = 4 x$ B、 $y = - x$ C、 $y = - \frac{5}{x}$ D、 $y = 6 x + 1$

查看试题解析
2. 要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5 $c m$ ，6 $c m$ ，9 $c m$ ，另一个三角形的最长边长为4.5 $c m$ ，则它的最短边长是（）

A、 $1.5 c m$ B、 $2.5 c m$ C、 $3 c m$ D、 $4 c m$

查看试题解析
3. 若点 $(- 2 ， y_{1})$ ， $(- 1 ， y_{2})$ ， $(3 ， y_{3})$ 在双曲线上 $y = - \frac{1}{x}$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
4. 如图，在边长为1的小正方形网格中，点 $A ， B ， C$ 都在这些小正方形的顶点上，则 $∠ C B A$ 的余弦值是（）

A、 $\frac{3}{13}$ B、 $\frac{2}{3}$ C、 $\frac{2 \sqrt{13}}{13}$ D、 $\frac{3 \sqrt{13}}{13}$

查看试题解析
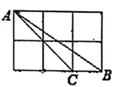5. 如图，所示的计算程序中，y与x之间的函数关系对应的图象所在的象限是（）

A、第一象限 B、第一、三象限 C、第二、四象限 D、第一、四象限

查看试题解析
6. 如图， $Δ A B C$ 中， $∠ C = 80^{\circ}$ ， $A C = 4$ ， $B C = 6$ .将 $Δ A B C$ 沿图示中的虚线剪开，按下面四种方式剪下的阴影三角形与原三角形相似的是（）

A、①②③ B、②③④ C、①② D、④

查看试题解析
7. 反比例函数 $y = \frac{a}{x}$ 与正比例函数 $y = a x + a$ 在同一坐标系中的大致图象可能是（）

A、 B、 C、 D、

查看试题解析
8. 把两个同样大小的含45°角的三角板如图所示放置，其中一个三角板的锐角顶点与另一个的直角顶点重合于点 $D$ ，且另三个锐角顶点 $A ， B ， C$ 在同一直线上，若 $A D = 2$ ，则 $A B$ 的长是（）

A、 $\sqrt{3} - \sqrt{2}$ B、 $\sqrt{2} - 1$ C、0.5 D、 $\sqrt{3} - 1$

查看试题解析
9. 如图，由一些完全相同的小正方体搭成的几何体的左视图和俯视图，则这个几何体的主视图不可能是（）

A、 B、 C、 D、

查看试题解析
10. 如图， $R t Δ A O B$ 中， $∠ A O B = 90 °$ ，顶点 $A$ ， $B$ 分别在反比例函数 $y = \frac{2}{x}$ （ $x > 0$ ）与 $y = - \frac{8}{x}$ （ $x < 0$ ）的图象上.则下列等式成立的是（）

A、 $\sin ∠ B A O = \frac{\sqrt{5}}{5}$ B、 $\cos ∠ B A O = \frac{\sqrt{5}}{2}$ C、 $\tan ∠ B A O = 2$ D、 $\sin ∠ A B O = \frac{1}{4}$

查看试题解析

二、填空题

11. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A B = 11$ ， $B C = 6$ ，则 $\sin A$ 的值是．

查看试题解析
12. 如图， $Δ A' B' C'$ 是 $Δ A B C$ 以点 $O$ 为位似中心经过位似变换得到的，若 $O B' ： B' B = 2 ： 1$ ，则 $Δ A' B' C'$ 的周长与 $Δ A B C$ 的周长比是．

查看试题解析
13. 公元前3世纪，古希腊科学家阿基米德发现了杠杆平衡，后来人们归纳出为“杠杆原理”.已知，手压压水井的阻力和阻力臂分别是90 $N$ 和0.3 $m$ ，则动力 $F_{1}$ （单位： $N$ ）与动力臂 $L_{1}$ （单位： $m$ ）之间的函数解析式是．

查看试题解析
14. 一个几何体的三视图如图所示，根据图中数据，计算出该几何体的表面积是．

查看试题解析
15. 反比例函数 $y = - \frac{4}{x}$ 的图象经过点 $A (- 4 ， n)$ ， $B (m ， 4)$ ，点 $C$ 是 $y$ 轴上一动点.当 $C A + C B$ 的值最小时，点 $C$ 的坐标是．

查看试题解析

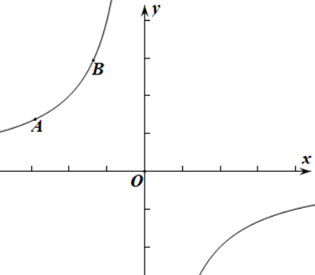
三、解答题

16. 画出如图所示几何体的三视图．

查看试题解析
17. 如图，已知双曲线 $y_{1} = \frac{k}{x}$ 与直线 $y_{2} = a x + b$ 交于点 $A (1 ， 4)$ 和点 $B (m ， - 1)$

(1)、求双曲线的解析式；

(2)、直接写出不等式 $a x + b < \frac{k}{x}$ 的解集

查看试题解析
18. 知识改变世界，科技改变生活，导航装备的不断更新极大方便了人们的出行.周末，小强一家到 $B ， C$ 两处景区游玩，他们从家 $A$ 处出发，向正西行驶160 $k m$ 到达 $B$ 处，测得 $C$ 处在 $B$ 处的北偏西15°方向上，出发时测得 $C$ 处在 $A$ 处的北偏西60°方向上

(1)、填空： $∠ C =$ 度；

(2)、求 $B$ 处到 $C$ 处的距离即 $B C$ 的长度（结果保留根号）

查看试题解析
19. 放寒假，小明的爸爸把油箱注满油后准备驾驶汽车到距家300 $k m$ 的学校接小明，在接到小明后立即按原路返回，已知小明爸爸汽车油箱的容积为70 $L$ ，请回答下列问题：

(1)、写出油箱注满油后，汽车能够行使的总路程 $s (k m)$ 与平均耗油量 $x (L / k m)$ 之间的函数关系式；

(2)、小明的爸爸以平均每千米耗油0.1 $L$ 的速度驾驶汽车到达学校，在返回时由于下雨，小明的爸爸降低了车速，此时每千米的耗油量增加了一倍，如果小明的爸爸始终以此速度行使，油箱里的油是否够回到家？如果不够用，请通过计算说明至少还需加多少油？

查看试题解析
20. 如图，矩形 $A B C D$ 中， $A B = 8$ ， $B C = 7$ ，点 $P$ 为边 $B C$ 延长线上的一点，过 $D P$ 的中点 $E$ 作 $E M ⊥ D P$ 交边 $D C$ 于 $M$ ，交边 $A B$ 的延长线于 $N$ ， $E F / / B C$ ，交边 $A B$ 于 $F$ ，交边 $D C$ 于 $H$

(1)、当 $C P = 4$ 时，求 $\frac{E M}{E N}$ 的值；

(2)、猜想 $M N$ 与 $D P$ 的数量关系，并证明你的猜想

查看试题解析
21. （阅读材料）某校九年级数学课外兴趣探究小组在学习完《第二十八章锐角三角函数》后，利用所学知识进行深度探究，得到以下正确的等量关系式：
$\sin (α + β) = \sin α \cdot \cos β + \cos α \cdot \sin β$ ， $\sin (α - β) = \sin α \cdot \cos β - \cos α \cdot \sin β$

$\cos (α + β) = \cos α \cdot \cos β - \sin α \cdot \sin β$ ， $\cos (α - β) = \cos α \cdot \cos β + \sin α \cdot \sin β$

$\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \cdot \tan β}$ ， $\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \cdot \tan β}$ ，

(1)、（理解应用）请你利用以上信息求下列各式的值：
$\sin 15^{°}$ ；

(2)、 $\cos 105^{°}$

(3)、（拓展应用）
为了求出海岛上的山峰 $A B$ 的高度，在 $D$ 处和 $F$ 处树立标杆 $C D$ 和 $E F$ ，标杆的高都是3丈， $D ， F$ 两处相隔1000步（1步等于6尺），并且 $A B ， C D$ 和 $E F$ 在同一平面内，在标杆 $C D$ 的顶端 $C$ 处测得山峰顶端 $A$ 的仰角75°，在标杆 $E F$ 的顶端 $E$ 处测得山峰顶端 $A$ 的仰角30°，山峰的高度即 $A B$ 的长是多少步？（结果保留整数）（参考数据： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7 ， \sqrt{5} \approx 2.2 ， \sqrt{6} \approx 2.4$ ）

查看试题解析
22. 如图1，已知 $R t Δ A B C$ 中， $∠ A C B = 90^{\circ}$ ， $A C = 2$ ， $B C = 2 \sqrt{3}$ ，它在平面直角坐标系中位置如图所示，点 $A ， C$ 在 $x$ 轴的负半轴上（点 $C$ 在点 $A$ 的右侧），顶点 $B$ 在第二象限，将 $Δ A B C$ 沿 $A B$ 所在的直线翻折，点 $C$ 落在点 $D$ 位置

(1)、若点 $C$ 坐标为 $(- 1 ， 0)$ 时，求点 $D$ 的坐标；

(2)、若点 $B$ 和点 $D$ 在同一个反比例函数的图象上，求点 $C$ 坐标；

(3)、如图2，将四边形 $B C A D$ 向左平移，平移后的四边形记作四边形 $B_{1} C_{1} A_{1} D_{1}$ ，过点 $D_{1}$ 的反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与 $C B$ 的延长线交于点 $E$ ，则在平移过程中，是否存在这样的 $k$ ，使得以点 $E ， B_{1} ， D$ 为顶点的三角形是直角三角形且点 $D_{1} ， B_{1} ， E$ 在同一条直线上？若存在，求出 $k$ 的值；若不存在，请说明理由

查看试题解析