山东省济南市商河县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
1. 图中几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 一元二次方程3x2﹣x=0的解是( )A、x= B、x1=0,x2=3 C、x1=0,x2= D、x=03. 如图,在△ABC中,∠C=90°,cosA= ,AB=10,AC的长是( )
2. 一元二次方程3x2﹣x=0的解是( )A、x= B、x1=0,x2=3 C、x1=0,x2= D、x=03. 如图,在△ABC中,∠C=90°,cosA= ,AB=10,AC的长是( )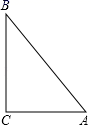 A、3 B、6 C、9 D、124. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形5. 如图,△ABC中,DE∥BC , 则下列等式中不成立的是( )
A、3 B、6 C、9 D、124. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形5. 如图,△ABC中,DE∥BC , 则下列等式中不成立的是( )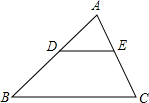 A、 B、 C、 D、6. 下列二次函数中有一个函数的图象与x轴有两个不同的交点,这个函数是( )A、 B、 C、 D、7. 现有两组相同的牌,每组三张且大小一样,三张牌的牌面数字分别是1、2、3,从每组牌中各摸出一张牌.两张牌的牌面数字之和等于4的概率是( )A、 B、 C、 D、8. 反比例函数y= 和一次函数y=kx-k在同一坐标系中的图象大致是( )A、
A、 B、 C、 D、6. 下列二次函数中有一个函数的图象与x轴有两个不同的交点,这个函数是( )A、 B、 C、 D、7. 现有两组相同的牌,每组三张且大小一样,三张牌的牌面数字分别是1、2、3,从每组牌中各摸出一张牌.两张牌的牌面数字之和等于4的概率是( )A、 B、 C、 D、8. 反比例函数y= 和一次函数y=kx-k在同一坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 9. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V( )的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将会爆炸,为了安全起见,气球的体积应( )
9. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V( )的反比例函数,其图象如图所示,当气球内的气压大于120kPa时,气球将会爆炸,为了安全起见,气球的体积应( )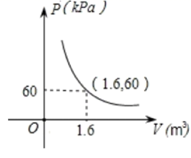 A、不大于 B、大于 C、不小于 D、小于10. 一元二次方程x2+bx﹣2=0中,若b<0,则这个方程根的情况是( )A、有两个正根 B、有一正根一负根且正根的绝对值大 C、有两个负根 D、有一正根一负根且负根的绝对值大11. 如图,在△ABC中,DE∥BC , BE和CD相交于点F , 且S△EFC=3S△EFD , 则S△ADE:S△ABC的值为( )
A、不大于 B、大于 C、不小于 D、小于10. 一元二次方程x2+bx﹣2=0中,若b<0,则这个方程根的情况是( )A、有两个正根 B、有一正根一负根且正根的绝对值大 C、有两个负根 D、有一正根一负根且负根的绝对值大11. 如图,在△ABC中,DE∥BC , BE和CD相交于点F , 且S△EFC=3S△EFD , 则S△ADE:S△ABC的值为( )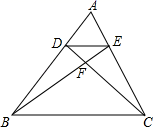 A、1:3 B、1:8 C、1:9 D、1:412. 二次函数 ( 是常数, )的自变量 与函数值 的部分对应值如下表:
A、1:3 B、1:8 C、1:9 D、1:412. 二次函数 ( 是常数, )的自变量 与函数值 的部分对应值如下表:…
0
1
2
…
…
…
且当 时,与其对应的函数值 .有下列结论:① ;② 和3是关于 的方程 的两个根;③ .其中,正确结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
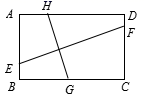
13. 计算:2sin30°+tan45°= .14. 将二次函数 化成 的形式,则y= .15. 已知三角形的两边分别是3和4,第三边的数值是方程x2﹣9x+14=0的根,则这个三角形的周长为 .16. 小亮和他弟弟在阳光下散步,小亮的身高为1.75米,他的影子长2米.若此时他的弟弟的影子长为1.6米,则弟弟的身高为米.17. 如图,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF︰GH= .
 18. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是.
18. 如图,已知直线y=﹣x+2分别与x轴,y轴交于A,B两点,与双曲线y= 交于E,F两点,若AB=2EF,则k的值是.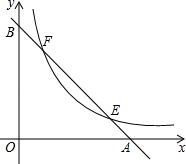
三、解答题
-
19. 计算: .20. 解方程:(x+3)(x﹣6)=﹣8.21. 如图,在▱ABCD中,作对角线BD的垂直平分线EF,垂足为O,分别交AD,BC于E,F,连接BE,DF.求证:四边形BFDE是菱形.
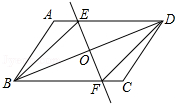 22. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).
22. 如图,海面上一艘船由西向东航行,在A处测得正东方向上一座灯塔的最高点C的仰角为31°,再向东继续航行30m到达B处,测得该灯塔的最高点C的仰角为45°,根据测得的数据,计算这座灯塔的高度CD(结果取整数).参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60.
 23. 某超市销售一种成本为每千克40元的水产品,经市场分析,若按每千克50元销售,一个月能销售出500千克;销售单价每涨价1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:(1)、每千克涨价x元,那么销售量表示为千克,涨价后每千克利润为元(用含x的代数式表示.)(2)、要使得月销售利润达到8000元,又要“薄利多销”,销售单价应定为多少?这时应进货多少千克?24. 十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
23. 某超市销售一种成本为每千克40元的水产品,经市场分析,若按每千克50元销售,一个月能销售出500千克;销售单价每涨价1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:(1)、每千克涨价x元,那么销售量表示为千克,涨价后每千克利润为元(用含x的代数式表示.)(2)、要使得月销售利润达到8000元,又要“薄利多销”,销售单价应定为多少?这时应进货多少千克?24. 十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
 (1)、五届艺术节共有个班级表演这些节日,班数的中位数为 , 在扇形统计图中,第四届班级数的扇形圆心角的度数为;(2)、补全折线统计图;(3)、第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用 , , , 表示).利用树状图或表格求出该班选择 和 两项的概率.25. 如图
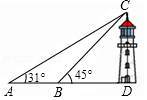
(1)、五届艺术节共有个班级表演这些节日,班数的中位数为 , 在扇形统计图中,第四届班级数的扇形圆心角的度数为;(2)、补全折线统计图;(3)、第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用 , , , 表示).利用树状图或表格求出该班选择 和 两项的概率.25. 如图 (1)、如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE,求证:CE=CF;(2)、如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD;(3)、运用(1)(2)解答中所积累的经验和知识,完成下题:
(1)、如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE,求证:CE=CF;(2)、如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD;(3)、运用(1)(2)解答中所积累的经验和知识,完成下题:如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10, 求直角梯形ABCD的面积.
26. 如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.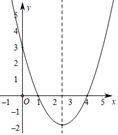 (1)、求该抛物线的解析式;(2)、如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.(3)、在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.
(1)、求该抛物线的解析式;(2)、如图,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.(3)、在(2)的条件下,点Q是线段OB上一动点,当△BPQ与△BAC相似时,求点Q的坐标.