山东省德州市宁津县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-05 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列说法正确的是（）

A、25人中至少有3人的出生月份相同 B、任意抛掷一枚均匀的1元硬币，若上一次正面朝上，则下一次一定反面朝上 C、天气预报说明天降雨的概率为10%，则明天一定是晴天 D、任意抛掷一枚均匀的骰子，掷出的点数小于3的概率是 $\frac{1}{2}$

查看试题解析
3. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 53 °$ ，若 $B C = m$ ，则AB的长为（）

A、 $\frac{m}{\cos 53 °}$ B、 $m \cdot \cos 53 °$ C、 $m \cdot \sin 53 °$ D、 $m \cdot \tan 53 °$

查看试题解析
4. 方程（m﹣1）x²﹣2mx+m﹣1＝0中，当m取什么范围内的值时，方程有两个不相等的实数根？（）

A、m＞ $\frac{1}{2}$ B、m＞ $\frac{1}{2}$ 且m≠1 C、m＜ $\frac{1}{2}$ D、m≠1

查看试题解析
5. 将 $y = 2 x^{2} - 8 x - 1$ 化成 $y = a {(x + m)}^{2} + n$ 的形式为（）

A、 $y = 2 {(x - 2)}^{2} + 7$ B、 $y = 2 {(x - 4)}^{2} - 1$ C、 $y = 2 {(x - 2)}^{2} - 9$ D、 $y = 2 {(x - 4)}^{2} - 7$

查看试题解析
6. 若 $\frac{x}{2} = \frac{y}{7} = \frac{z}{5}$ ，则 $\frac{x + y - z}{x}$ 的值是（　　）

A、1 B、2 C、3 D、4

查看试题解析
7. 为了宣传垃圾分类，童威写了一篇倡议书，决定用微博转发的方式传播.他设计了如下的传播规则：将倡议书发表在自己的微博上，再邀请n个好友转发，每个好友转发之后，又邀请n个互不相同的好友转发，依次类推.已知经过两轮转发后，共有111个人参与了宣传活动，则n的值为（）

A、9 B、10 C、11 D、12

查看试题解析
8. 如图，AB是⊙O的弦，半径OC⊥AB ， D为圆周上一点，若 $\overset{⌢}{B C}$ 的度数为50°，则∠ADC的度数为（）

A、20° B、25° C、30° D、50°

查看试题解析
9. 如图，将 $△ A O B$ 绕点O按逆时针方向旋转 $45 °$ 后得到 $△ A^{'} O B^{'}$ ，若 $∠ A O B = 15 °$ ，则 $∠ A O B^{'}$ 的度数是（）

A、30° B、35° C、40° D、45°

查看试题解析
10. 如图是小玲设计用手电来测家附近“新华大厦”高度的示意图．点 $P$ 处放一水平的平面镜，光线从点 $A$ 出发经平面镜反射后刚好射到大厦 $C D$ 的顶端 $C$ 处，已知 $A B ⊥ B D ， C D ⊥ B D$ ，且测得 $A B = 1.2$ 米， $B P = 1.8$ 米， $P D = 24$ 米，那么该大厦的高度约为（）

A、8米 B、16米 C、24米 D、36米

查看试题解析
11. 如图直线y＝mx与双曲线y= $\frac{k}{x}$ 交于点A、B ，过A作AM⊥x轴于M点，连接BM ，若S_△_AMB＝2，则k的值是（）

A、1 B、2 C、3 D、4

查看试题解析
12. 已知二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则下列结论： ① abc＜0；② 2a＋b＝0； ③ b²－4ac＜0；④ 9a+3b+c＞0； ⑤ c+8a＜0.正确的结论有（）.

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

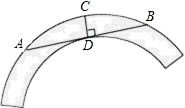
13. 已知 $x_{1}$ ， $x_{2}$ 是关于 $x$ 的方程 $x^{2} + k x - 3 = 0$ 的两根，且满足 $x_{1} + x_{2} - 3 x_{1} x_{2} = 4$ ，则 $k$ 的值为.

查看试题解析
14. 已知反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象与经过原点的直线 $L$ 相交于点 $A 、 B$ 两点，若点 $A$ 的坐标为 $(1 ， 2)$ ，则点 $B$ 的坐标为．

查看试题解析
15. 如图是一个圆环形黄花梨木摆件的残片，为求其外圆半径，小林在外圆上任取一点A，然后过点A作AB与残片的内圆相切于点D，作CD⊥AB交外圆于点C，测得CD＝15cm，AB＝60cm，则这个摆件的外圆半径是cm．

查看试题解析
16.
如图，三个小正方形的边长都为1，则图中阴影部分面积的和是（结果保留π）．

查看试题解析
17. 已知二次函数y＝ax²+3ax+c的图象与x轴的一个交点为（﹣4，0），则它与x轴的另一个交点的坐标是.

查看试题解析
18. 正 $△ A B C$ 的边长为 3cm ，边长为 1cm 的正 $△ R P Q$ 的顶点 R 与点 A 重合，点 P、Q 分别在 AC ， AB 上，将 $△ R P Q$ 沿边顺时针连续翻转（如图所示），直至点 P 第一次回到原来的位置，则点 P 运动路径的长为 cm （结果保留 $π$ ）

查看试题解析

三、解答题

19. 解方程：

(1)、 $x^{2} - 4 x + 1 = 0$ ．

(2)、 $9 {(x - 2)}^{2} = 4 {(x + 1)}^{2}$

查看试题解析
20. 如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 是弦， $D$ 是弧 $B C$ 的中点，过点 $D$ 作 $E F$ 垂直于直线 $A C ，$ 垂足为 $F$ ，交 $A B$ 的延长线于点 $E$ ．

(1)、求证： $E F$ 是 $⊙ O$ 的切线；

(2)、若 $A F = 6 ， E F = 8$ ，求 $⊙ O$ 的半径．

查看试题解析
21. 如图，一个转盘被分成3等分，每一份上各写有一个数字，随机转动转盘2次，第一次转到的数字数字为十位数字，第二次转到的数字为个位数字，2次转动后组成一个两位数（若指针停在等分线上则重新转一次）

(1)、用画树状图的方法求出转动后所有可能出现的两位数的个数．

(2)、甲、乙两人做游戏，约定得到的两位数是偶数时甲胜，否则乙胜，这个游戏公平吗？请说明理由．

查看试题解析
22. 如图，点C、D在线段AB上，△PCD是等边三角形，且CD²＝AD•BC ．

(1)、求证：△APD∽△PBC；

(2)、求∠APB的度数．

查看试题解析
23. 如图， $▱ A B C D$ 水平放在平面直角坐标系中，点 $A 、 D$ 的坐标分别为 $(- 2 ， 5) 、 (0 ， 1)$ ，点 $B (3 ， 5)$ 在函数 $y = \frac{k}{x} (k > 0)$ 的图象上．

(1)、求函数 $y = \frac{k}{x}$ 的表达式；

(2)、求点 $C$ 的坐标；

(3)、将 $▱ A B C D$ 沿 $x$ 轴正方向平移 $10$ 个单位后，判断点 $C$ 能否落在函数 $y = \frac{k}{x} (k > 0)$ 的图象上，请说明理由．

查看试题解析
24. 某体育可容纳四千人同时观看比赛，现C区有座位400个，某赛事试营销售阶段发现：当票价为80元时，可售出C区票280张，若每降价1元，可多售出6张票，设降价x元(x取正整数)时，可售出观赛座位票 $y$ 张.

(1)、求出y关于x的函数关系式；

(2)、设C区的总票价为W元，求W关于x的函数关系式，并求出W的最大值.

查看试题解析
25. 如图，在平面直角坐标系中抛物线 $y = a x^{2} + b x + c$ 交 $x$ 轴于点 $A 、 B$ ，交 $y$ 轴于点 $C$ ， $A 、 B$ 两点横坐标为-1和3， $C$ 点纵坐标为-4．

(1)、求抛物线的解析式；

(2)、动点 $D$ 在第四象限且在抛物线上，当 $△ B C D$ 面积最大时，求 $D$ 点坐标，并求 $△ B C D$ 面积的最大值．

查看试题解析