山东省德州市乐陵市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-05 类型:期末考试
一、单选题
-
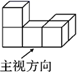
1. 关于x的一元二次方程x2+4x+k=0有两个相等的实数根,则k的值为( )A、k=4 B、k=﹣4 C、k≥﹣4 D、k≥42. 在反比例函数 的图象的每个象限内,y随x的增大而增大,则k值可以是( )A、-1 B、1 C、2 D、33. 如图是由5个完全相同的正方体组成的立体图形,它的主视图是( )
 A、
A、 B、
B、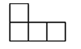 C、
C、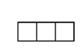 D、
D、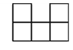 4. 如图, 中, , ,点 是 的外心.则 ( )
4. 如图, 中, , ,点 是 的外心.则 ( )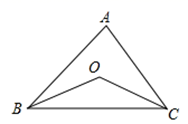 A、 B、 C、 D、5. 下列各说法中:①圆的每一条直径都是它的对称轴;②长度相等的两条弧是等弧;③相等的弦所对的弧也相等;④同弧所对的圆周角相等;⑤ 90°的圆周角所对的弦是直径;⑥任何一个三角形都有唯一的外接圆;其中正确的有( )A、3个 B、4个 C、5个 D、6个6. 如图,小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( )
A、 B、 C、 D、5. 下列各说法中:①圆的每一条直径都是它的对称轴;②长度相等的两条弧是等弧;③相等的弦所对的弧也相等;④同弧所对的圆周角相等;⑤ 90°的圆周角所对的弦是直径;⑥任何一个三角形都有唯一的外接圆;其中正确的有( )A、3个 B、4个 C、5个 D、6个6. 如图,小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA的高度与拉绳PB的长度相等.小明将PB拉到PB′的位置,测得∠PB′C=α(B′C为水平线),测角仪B′D的高度为1m,则旗杆PA的高度为( ) A、 m B、 m C、 m D、 m7. 如图, 是函数 的图像上关于原点对称的任意两点, 轴, 轴, 的面积记为 ,则( )
A、 m B、 m C、 m D、 m7. 如图, 是函数 的图像上关于原点对称的任意两点, 轴, 轴, 的面积记为 ,则( )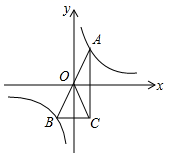 A、 B、 C、 D、8. 若函数 与 的图象如图所示,则函数 的大致图象为( )
A、 B、 C、 D、8. 若函数 与 的图象如图所示,则函数 的大致图象为( )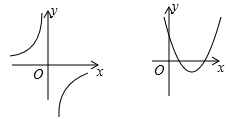 A、
A、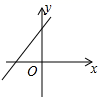 B、
B、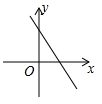 C、
C、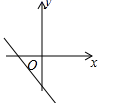 D、
D、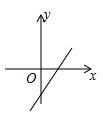 9. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )
9. 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则tan∠ABC的值为( )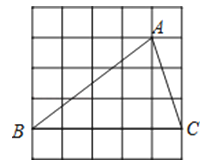 A、 B、 C、 D、110. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )
A、 B、 C、 D、110. 学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,CD⊥BD,垂足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为( )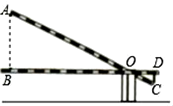 A、0.2m B、0.3m C、0.4m D、0.5m11. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A、0.2m B、0.3m C、0.4m D、0.5m11. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( ) A、
A、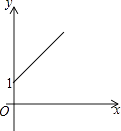 B、
B、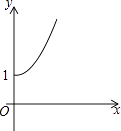 C、
C、 D、
D、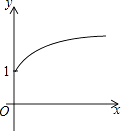 12. 在下列函数图象上任取不同两点 , ,一定能使 成立的是( )A、 B、 C、 D、13. 如图,点 的坐标是 , 是等边角形,点 在第一象限,若反比例函数 的图象经过点 ,则 的值是( )
12. 在下列函数图象上任取不同两点 , ,一定能使 成立的是( )A、 B、 C、 D、13. 如图,点 的坐标是 , 是等边角形,点 在第一象限,若反比例函数 的图象经过点 ,则 的值是( )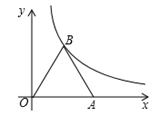 A、1 B、3 C、 D、14. 如图,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
A、1 B、3 C、 D、14. 如图,以原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )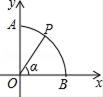 A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)15. 如图,在 中, 两个顶点在 轴的上方,点 的坐标是 .以点 为位似中心,在 轴的下方作 的位似,图形 ,使得 的边长是 的边长的2倍.设点 的横坐标是-3,则点 的横坐标是( )
A、(sinα,sinα) B、(cosα,cosα) C、(cosα,sinα) D、(sinα,cosα)15. 如图,在 中, 两个顶点在 轴的上方,点 的坐标是 .以点 为位似中心,在 轴的下方作 的位似,图形 ,使得 的边长是 的边长的2倍.设点 的横坐标是-3,则点 的横坐标是( )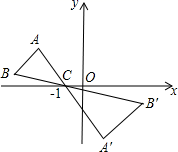 A、2 B、3 C、4 D、516. 如图,正方形ABCD中,BE=FC , CF=2FD , AE、BF交于点G , 连接AF , 给出下列结论:①AE⊥BF; ②AE=BF; ③BG= GE; ④S四边形CEGF=S△ABG , 其中正确的个数为( )
A、2 B、3 C、4 D、516. 如图,正方形ABCD中,BE=FC , CF=2FD , AE、BF交于点G , 连接AF , 给出下列结论:①AE⊥BF; ②AE=BF; ③BG= GE; ④S四边形CEGF=S△ABG , 其中正确的个数为( )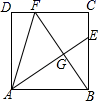 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 方程2x2=x的根是 .18. 汽车刹车后行驶的距离 (单位: )关于行驶的时间 (单位: )的函数解析式是 .汽车刹车后到停下来前进了 .19. 如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为 .
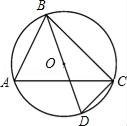 20. 如图,在四边形 中, , ,则 的度数为 .
20. 如图,在四边形 中, , ,则 的度数为 .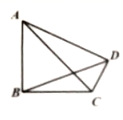 21. 婷婷和她妈妈玩猜拳游戏.规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时婷婷获胜.那么,婷婷获胜的概率为.
21. 婷婷和她妈妈玩猜拳游戏.规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时婷婷获胜.那么,婷婷获胜的概率为. 22. 某园进行改造,现需要修建一些如图所示圆形(不完整)的门,根据实际需要该门的最高点C距离地面的高度为2.5m,宽度AB为1m,则该圆形门的半径应为m.
22. 某园进行改造,现需要修建一些如图所示圆形(不完整)的门,根据实际需要该门的最高点C距离地面的高度为2.5m,宽度AB为1m,则该圆形门的半径应为m.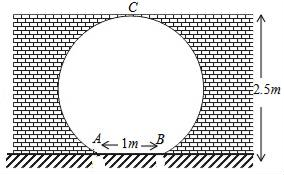 23. 如图,边长为 的正六边形在足够长的桌面上滚动(没有滑动)一周,则它的中心 点所经过的路径长为 .
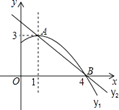
23. 如图,边长为 的正六边形在足够长的桌面上滚动(没有滑动)一周,则它的中心 点所经过的路径长为 .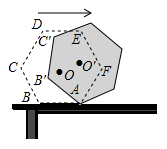 24. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
24. 如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,其中正确的是 .
三、解答题
-
25. 已知关于 的一元二次方程 有两个实数根 , .(1)、求 的取值范围:(2)、当 时,求 的值.26. 为了了解全校 名同学对学校设置的体操、篮球、足球、跑步、舞蹈等课外活动项目的喜爱情况,在全校范围内随机抽取了若干名同学,对他们喜爱的项目(每人选一项)进行了问卷调查,将数据进行了统计,并绘制成了如图所示的条形统计图和扇形统计图(均不完整),请回答下列问题.
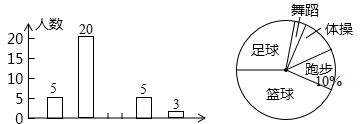 (1)、在这次问卷调查中,共抽查了名同学;(2)、补全条形统计图;(3)、估计该校 名同学中喜爱足球活动的人数;(4)、在体操社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加体操大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.27. 如图,在平面直角坐标系xOy中,反比例函数 的图象过等边三角形BOC的顶点B, OC=2,点A在反比例函数图象上,连接AC,AO.
(1)、在这次问卷调查中,共抽查了名同学;(2)、补全条形统计图;(3)、估计该校 名同学中喜爱足球活动的人数;(4)、在体操社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加体操大赛.用树状图或列表法求恰好选中甲、乙两位同学的概率.27. 如图,在平面直角坐标系xOy中,反比例函数 的图象过等边三角形BOC的顶点B, OC=2,点A在反比例函数图象上,连接AC,AO.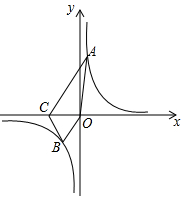 (1)、求反比例函数 的表达式;(2)、若四边形ACBO的面积是 ,求点A的坐标.28. 某型号飞机的机翼形状如图所示,已知 所在直线互相平行且都与 所在直线垂直, . , , , .求 的长度(参考数 , , , , , )
(1)、求反比例函数 的表达式;(2)、若四边形ACBO的面积是 ,求点A的坐标.28. 某型号飞机的机翼形状如图所示,已知 所在直线互相平行且都与 所在直线垂直, . , , , .求 的长度(参考数 , , , , , )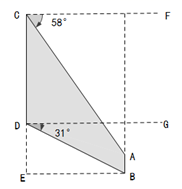 29. 如图, 是 的直径, 过 的中点 . ,垂足为 .
29. 如图, 是 的直径, 过 的中点 . ,垂足为 .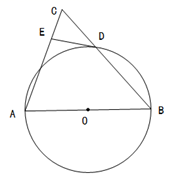 (1)、求证:直线 是 的切线;(2)、若 , 的直径为 ,求 的长及 的值.30. 如图
(1)、求证:直线 是 的切线;(2)、若 , 的直径为 ,求 的长及 的值.30. 如图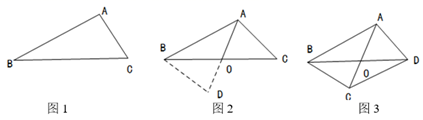 (1)、某学校“学习落实”数学兴趣小组遇到这样一个题目:如图1,在 中,点 在线段 上, , , , ,求 的长.经过数学小组成员讨论发现,过点 作 ,交 的延长线于点 ,通过构造 就可以解决问题(如图2)请回答:∠ADB=°,AB= .(2)、请参考以上解决思路,解决问题:如图 在四边形 中对角线 与 相交于点 , , , , .求 的长.31. 如图1,抛物线 与 轴交于点 和点 ,与 轴交于点 ,且 满足 ,若对称轴在 轴的右侧.
(1)、某学校“学习落实”数学兴趣小组遇到这样一个题目:如图1,在 中,点 在线段 上, , , , ,求 的长.经过数学小组成员讨论发现,过点 作 ,交 的延长线于点 ,通过构造 就可以解决问题(如图2)请回答:∠ADB=°,AB= .(2)、请参考以上解决思路,解决问题:如图 在四边形 中对角线 与 相交于点 , , , , .求 的长.31. 如图1,抛物线 与 轴交于点 和点 ,与 轴交于点 ,且 满足 ,若对称轴在 轴的右侧.
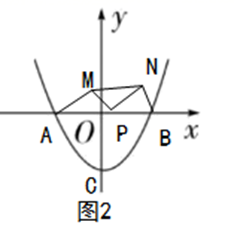 (1)、求抛物线的解析式.(2)、如图2,若点 为线段 上的一动点(不与 重合),分别以 、 为斜边,在直线 的同侧作等腰直角三角形 和 ,试确定 面积最大时 点的坐标.(3)、若 , 是抛物线上的两点,当 , 时,均有 ,求 的取值范围.
(1)、求抛物线的解析式.(2)、如图2,若点 为线段 上的一动点(不与 重合),分别以 、 为斜边,在直线 的同侧作等腰直角三角形 和 ,试确定 面积最大时 点的坐标.(3)、若 , 是抛物线上的两点,当 , 时,均有 ,求 的取值范围.