上海金山初中2020-2021学年九年级上学期数学9月月考试卷
试卷更新日期:2020-12-05 类型:月考试卷
一、单选题
-
1. 如图,将图形用放大镜放大,应该属于( ).
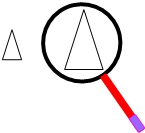 A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 如图,在 中, ,且 ,则 的值为( )
A、平移变换 B、相似变换 C、旋转变换 D、对称变换2. 如图,在 中, ,且 ,则 的值为( )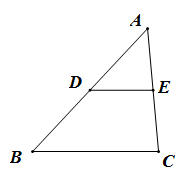 A、1 B、2 C、 D、3. 已知 ,则 ( )A、2 B、 C、3 D、4. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 ,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A、1 B、2 C、 D、3. 已知 ,则 ( )A、2 B、 C、3 D、4. 要制作两个形状相同的三角形框架,其中一个三角形的三边长分别为 , 和 ,另一个三角形的最短边长为2.5 cm,则它的最长边为( )
A、3cm B、4cm C、4.5cm D、5cm5. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB’,则点B的对应点B’的坐标是( ) A、(1,0) B、( , ) C、(1, ) D、(-1, )6. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法中错误的是( )
A、(1,0) B、( , ) C、(1, ) D、(-1, )6. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,以下说法中错误的是( )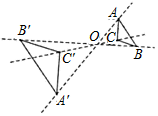 A、 B、点C,点O、点C′三点在同一直线上 C、 D、7. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、点C,点O、点C′三点在同一直线上 C、 D、7. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处8. 如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )
A、①处 B、②处 C、③处 D、④处8. 如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为( )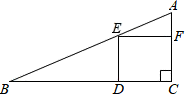 A、100cm2 B、150cm2 C、170cm2 D、200cm29. 如图,在 中,点D为 边上的一点,且 , ,过点D作 , 交 于点E,若 ,则 的面积为( )
A、100cm2 B、150cm2 C、170cm2 D、200cm29. 如图,在 中,点D为 边上的一点,且 , ,过点D作 , 交 于点E,若 ,则 的面积为( )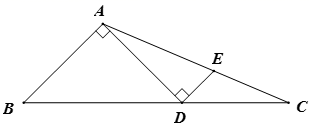 A、 B、 C、 D、10. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( )
A、 B、 C、 D、10. 如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF= AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( ) A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题
-
11. 直线CD∥EF,若OC=3,CE=4,则 的值是 .
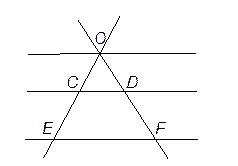 12. 如图,以点O为位似中心,将 放大后得到 , ,则 .
12. 如图,以点O为位似中心,将 放大后得到 , ,则 .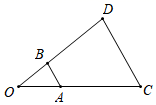 13. 如图,将等边 放在平面直角坐标系中,点A的坐标为 ,点B在第一象限,将等边 绕点O顺时针旋转180°得到 ,则点 的坐标是 .
13. 如图,将等边 放在平面直角坐标系中,点A的坐标为 ,点B在第一象限,将等边 绕点O顺时针旋转180°得到 ,则点 的坐标是 . 14. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .
14. 已知:如图,△ABC的面积为12,点D、E分别是边AB、AC的中点,则四边形BCED的面积为 .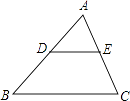 15. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”
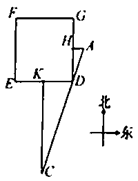
15. 《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步而见木?”用今天的话说,大意是:如图, 是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门 位于 的中点,南门 位于 的中点,出东门15步的 处有一树木,求出南门多少步恰好看到位于 处的树木(即点 在直线 上)?请你计算 的长为步.
 16. 如图,正方形纸片 的边长为12, 是边 上一点,连接 .折叠该纸片,使点 落在 上的 点,并使折痕经过点 ,得到折痕 ,点 在 上.若 ,则 的长为.
16. 如图,正方形纸片 的边长为12, 是边 上一点,连接 .折叠该纸片,使点 落在 上的 点,并使折痕经过点 ,得到折痕 ,点 在 上.若 ,则 的长为.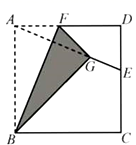 17. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
17. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号) 18. 如图,在 中, .若进行以下操作,在边 上从左到右依次取点 ,过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ,则 .
18. 如图,在 中, .若进行以下操作,在边 上从左到右依次取点 ,过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ,则 .
三、解答题
-
19. 已知,如图 ,求 和 的长.
 20. 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,如果木杆 长 ,它的影长 为 ,测得 为 ,求金字塔的高度 .
20. 据史料记载,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图,如果木杆 长 ,它的影长 为 ,测得 为 ,求金字塔的高度 . 21. 如图,在 中, =8, =4, =6, , 是 的平分线, 交 于点 ,求 的长.
21. 如图,在 中, =8, =4, =6, , 是 的平分线, 交 于点 ,求 的长. 22. 如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
22. 如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3. (1)、求EC的值;(2)、求证:AD•AG=AF•AB.23. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.
(1)、求EC的值;(2)、求证:AD•AG=AF•AB.23. 如图, ,DB平分∠ADC,过点B作 交AD于M.连接CM交DB于N.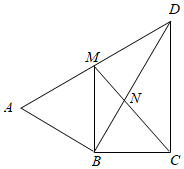 (1)、求证: ;(2)、若 ,求MN的长.24. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.
(1)、求证: ;(2)、若 ,求MN的长.24. 根据相似多边形的定义,我们把四个角分别相等,四条边成比例的两个凸四边形叫做相似四边形,相似四边形对应边的比叫做相似比.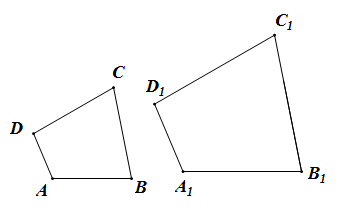 (1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否符合题意(直接在横线上填写“真”或“假”).
(1)、某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否符合题意(直接在横线上填写“真”或“假”).①四条边成比例的两个凸四边形相似;(命题)
②三个角分别相等的两个凸四边形相似;(命题)
③两个大小不同的正方形相似.(命题)
(2)、如图,在四边形 和四边形 中, , ,求证:四边形 与四边形 相似.25. 如图,在正方形ABCD中,点E,F分别是边AD,BC的中点,连接DF,过点E作EH⊥DF,垂足为H,EH的延长线交DC于点G. (1)、猜想DG与CF的数量关系,并证明你的结论;(2)、过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.
(1)、猜想DG与CF的数量关系,并证明你的结论;(2)、过点H作MN∥CD,分别交AD,BC于点M,N,若正方形ABCD的边长为10,点P是MN上一点,求△PDC周长的最小值.