山西省晋中市2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-12-05 类型:月考试卷
一、单选题
-
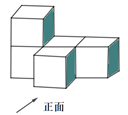
1. -4的绝对值是( )A、-4 B、4 C、±4 D、2. 如图所示的是一个由5块大小相同的小正方体搭建成的几何体,则它的左视图是( )
 A、
A、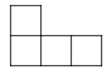 B、
B、 C、
C、 D、
D、 3. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、4. 2020年5月5日,由中国航天科技集团一院负责研制的长征五号B运载火箭在中国文昌航天发射场成功首飞,将我国新一代载人飞船试验船送入了预定轨道.它的意义重大,进一步奠定了长征五号系列运载火箭在世界现役火箭运载能力第一梯队中的地位.长征五号运载火箭擅于跑长途,运送目的地包括大约3万6千公里外的地球同步轨道、38万公里外的月球,以及最近距离也有5千万公里的火星.3万6千公里用科学记数法可表示为( )
3. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、4. 2020年5月5日,由中国航天科技集团一院负责研制的长征五号B运载火箭在中国文昌航天发射场成功首飞,将我国新一代载人飞船试验船送入了预定轨道.它的意义重大,进一步奠定了长征五号系列运载火箭在世界现役火箭运载能力第一梯队中的地位.长征五号运载火箭擅于跑长途,运送目的地包括大约3万6千公里外的地球同步轨道、38万公里外的月球,以及最近距离也有5千万公里的火星.3万6千公里用科学记数法可表示为( ) A、 公里 B、 公里 C、 公里 D、 公里5. 下列计算正确的是( )A、 B、 C、 D、6. 《算经十书》是指汉、唐一千多年间的十部数学著作,它们曾经是隋唐时代国子监算学科的教科书,下列数学著作不属于《算经十书》的是( )A、《孙子算经》 B、《海岛算经》 C、《九章算术》 D、《算法统宗》7. 如图,已知 ,将一个含45°角的三角尺按图中方式放置, ,则 的度数为( )
A、 公里 B、 公里 C、 公里 D、 公里5. 下列计算正确的是( )A、 B、 C、 D、6. 《算经十书》是指汉、唐一千多年间的十部数学著作,它们曾经是隋唐时代国子监算学科的教科书,下列数学著作不属于《算经十书》的是( )A、《孙子算经》 B、《海岛算经》 C、《九章算术》 D、《算法统宗》7. 如图,已知 ,将一个含45°角的三角尺按图中方式放置, ,则 的度数为( )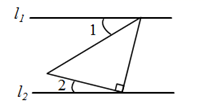 A、21° B、24° C、30° D、66°8. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定9. 已知关于 的二次函数 的图象关于直线 对称,则下列关系正确的是( )A、 B、 C、 的函数值一定大于 的函数值 D、若 ,则当 时,10. 若 的外接圆半径为R,内切圆半径为 ,则其内切圆的面积与 的面积比为( )A、 B、 C、 D、
A、21° B、24° C、30° D、66°8. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定9. 已知关于 的二次函数 的图象关于直线 对称,则下列关系正确的是( )A、 B、 C、 的函数值一定大于 的函数值 D、若 ,则当 时,10. 若 的外接圆半径为R,内切圆半径为 ,则其内切圆的面积与 的面积比为( )A、 B、 C、 D、二、填空题
-
11. 不等式组 的解集是 .12. 某校倡导学生在家积极参加劳动,开学后,统计了部分学生在家每天劳动时间的情况,结果如下表:
劳动时间(小时)
0.5
1
1.5
2
人数
10
12
6
2
则这些学生每天劳动时间的众数是小时.
13. 若太原高铁站2月份发送旅客2万人次,4月份发送旅客4.5万人次,且发送旅客月平均增长率相同,则该站这2个月发送旅客月平均增长率是 .14. 如图,在 中, , , 的平分线与以 为直径的 交于点D,E为 的中点,则 .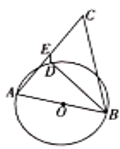 15. 如图,在Rt△ABC中,∠ACB=90°,BC=10,AC=20,D为AB的中点,连接CD,将△BCD沿CD翻折得到△B′CD,B′D交AC于点E.则 = .
15. 如图,在Rt△ABC中,∠ACB=90°,BC=10,AC=20,D为AB的中点,连接CD,将△BCD沿CD翻折得到△B′CD,B′D交AC于点E.则 = .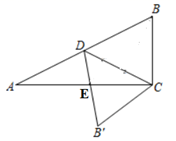
三、解答题
-
16.(1)、计算: .(2)、先化简,再求值: ,其中 .17. 如图1,已知 .请阅读下列作图过程,并解答所提出的问题.
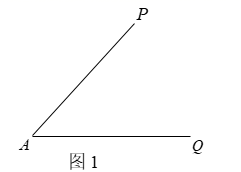
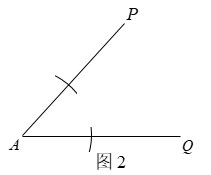
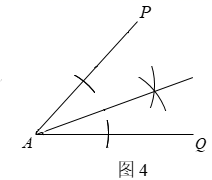
⑴如图2,以点A为圆心,任意长为半径画弧,分别与 , 交于B,C两点;
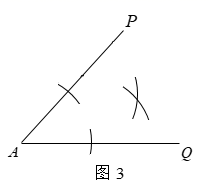
⑵如图3,分别以B,C两点为圆心,以大于 的长为半径画弧,两弧交于点D;
⑶如图4,作射线 ,连接 ,与 交于点E.
问题:
(1)、 的度数为 .(2)、若 ,求 的长.18. 随着疫情形势逐渐好转,各地企业陆续复工复产.为了促进员工进一步重视安全生产,掌握防疫知识,增强员工“科学防疫、安全生产”的意识,某企业在复工复产后组织开展了防疫安全知识竞赛活动.并随机抽取了部分员工的竞赛成绩(百分制)进行整理和分析(将分数分为四组:A. ,B. ,C. ,D. ,下面给出了部分信息:
抽取的员工竞赛成绩分布表
组别
分数/分
频数
A
B
12
C
6
D
3
扇形统计图
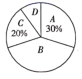
B组的成绩分别是88,86,80,86,84,82,80,86,82,84,88,86.(单位:分)
请解答下列问题:
(1)、 的值是 , B所占的百分比是 , B组数据的中位数是 .(2)、该企业共有320名员工参加了此次防疫安全知识竞赛活动,估计在本次活动中70分以下的人数.(3)、疫情期间,该企业的一些员工积极报名参加社区志愿者,挺身而出,服务于抗疫一线.为了进一步普及防疫知识,弘扬抗疫精神,该企业宣传部门打算从志愿者小王、小李、小张和小赵四人中随机抽取两人分享抗疫故事,请你用画树状图或列表的方法求出小王和小李被同时选中的概率.19. 端午节是中华民族的传统节日,全国各地素来都有端午节吃粽子的习俗.在今年端午节前夕,某商场采购了一批甲、乙两种品牌的粽子共600盒,其中采购甲品牌粽子花费7200元,采购乙品牌粽子花费9600元,已知每盒甲品牌粽子的进价是乙品牌粽子进价的1.5倍. (1)、求该商场采购的甲、乙两种品牌的粽子每盒进价分别是多少元.(2)、该商场原计划确定甲品牌粽子的售价为60元/盒,乙品牌粽子的售价为32元/盒.后调整销售策略,对甲品牌粽子进行打折销售,乙品牌粽子按原价售出.若要使购进的甲、乙两种品牌的粽子全部售出后所获利润不低于5600元,则每盒甲品牌粽子最低能打几折?20. 某“综合与实践”小组开展了测量本校对面山上一座古塔高度的实活动,他们制订了方案,并利用课余时间完成了实地测量.他们在该山脚的一块平地上,选择两个不同测点,分别测量山顶和塔顶的俯角,以及这两个测点之间的距离.为了减小测量误差,小组在测量俯角的度数以及两个测点之间的距离时,都分别测量了三次并取它们的平均值为测量结果,测量数据如下表(不完整).
(1)、求该商场采购的甲、乙两种品牌的粽子每盒进价分别是多少元.(2)、该商场原计划确定甲品牌粽子的售价为60元/盒,乙品牌粽子的售价为32元/盒.后调整销售策略,对甲品牌粽子进行打折销售,乙品牌粽子按原价售出.若要使购进的甲、乙两种品牌的粽子全部售出后所获利润不低于5600元,则每盒甲品牌粽子最低能打几折?20. 某“综合与实践”小组开展了测量本校对面山上一座古塔高度的实活动,他们制订了方案,并利用课余时间完成了实地测量.他们在该山脚的一块平地上,选择两个不同测点,分别测量山顶和塔顶的俯角,以及这两个测点之间的距离.为了减小测量误差,小组在测量俯角的度数以及两个测点之间的距离时,都分别测量了三次并取它们的平均值为测量结果,测量数据如下表(不完整).课题
测量山上塔的高度
测量工具
测量角度的仪器,皮尺等
测量示意图

说明:线段 CD 表示山高, CB 表示塔的高,测量角度的仪器的高度 ,端点B,C,D,A,E在同一竖直平面内,点D,C,B共线,点D,A,E共线.
测量数据
测量项目
第一次
第二次
第三次
平均值
的度数
63.6°
63.3°
63.3°
63.4°
的度数
29.9°
29.8°
30.3°
30°
的度数
44.9°
45.3°
44.8°
__________
A,E之间的距离
50.1m
49.8m
50.1m
__________
…
…
(1)、三次测量 的度数平均值是;A,E之间的距离的平均值是m.(2)、根据以上测量结果,请你帮助该“综合与实践”小组求出塔 BC 的高度.(结果精确到0.1m.参考数据: , , , , )
21. 阅读材料公元前5世纪,古希腊学者提出了一个问题:能否用尺规三等分一个任意角?为了解决这个问题,数学家们花费了大量的时间和精力.直到1837年,数学家们才证明了“三等分任意角”是不能用尺规完成的.那么.退而求其次,能不能借助一些特殊曲线解决这一问题呢?
在研究这个问题的过程中,古希腊数学家帕普斯给出的一方法如下:如图,将给定的锐角 置于平面直角坐标系中,角的一边 与 的图象交于点M, 在 轴上,以点M为圆心, 为半径画弧交 的图象于点N.分别过点M和N作 轴和 轴的平行线,两线相交于点E,F, 和 相交于点G,连接 得到 .
此时,爱思考的小明对这一结论展开了证明.下面是他的部分证明思路:
由题意,可知点M,N在反比例函数 的图象上,
先假设点M,N的坐标分别为 , ,
则点E,F的坐标可表示为 ,
则直线 的表达式为__.
由此,可以判断矩形 的顶点E在直线 上.
…
请根据以上材料,解答下列问题:
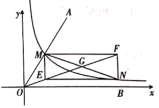 (1)、用含 , 的代数式表示直线 的表达式: .(2)、试接着上面小明所提供的证明思路,继续完成“ ”的证明.22. 综合与实践(1)、任意一个四边形 通过剪裁,都可以拼接成一个三角形,方法如下:如图1,E,F,G,H分别是边 , , , 的中点,连接 ,P是线段 的中点,连接 , ,沿线段 , , 剪开,将四边形 分成①,②,③,④四部分,按如图2所示的方式即可拼成一个无缝隙也不重叠的 .
(1)、用含 , 的代数式表示直线 的表达式: .(2)、试接着上面小明所提供的证明思路,继续完成“ ”的证明.22. 综合与实践(1)、任意一个四边形 通过剪裁,都可以拼接成一个三角形,方法如下:如图1,E,F,G,H分别是边 , , , 的中点,连接 ,P是线段 的中点,连接 , ,沿线段 , , 剪开,将四边形 分成①,②,③,④四部分,按如图2所示的方式即可拼成一个无缝隙也不重叠的 .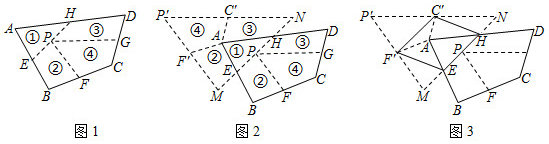
关于在拼接过程中用到的图形的变换,说法正确的是( )
A、①→①是轴对称 B、②→②是平移 C、③→③是中心对称 D、④→④是中心对称(2)、如图3,连接 , , ,判断四边形 的形状,并说明理由.(3)、若 是一个边长为4的等边三角形,则四边形 的对角线 的最小值为 .23. 综合与探究如图,抛物线 与 轴交于点A,B(点A在点B的左侧),与 轴正半轴交于点C.
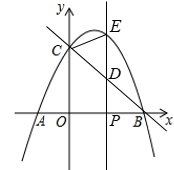
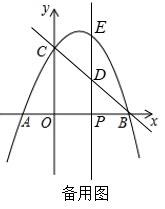 (1)、连接 , ,若 的面积为10,求抛物线的函数表达式.(2)、若P是 轴上的一个动点,过点P作垂直于 轴的直线分别交直线 和抛物线于点D和点E.设点P的横坐标为 .
(1)、连接 , ,若 的面积为10,求抛物线的函数表达式.(2)、若P是 轴上的一个动点,过点P作垂直于 轴的直线分别交直线 和抛物线于点D和点E.设点P的横坐标为 .①当点E在第一象限,且 时,求 的值.
②若D,E,P三个点中恰有一点是其他两点所连线段的中点(三点重合除外),则称D,E,P三点为“共生点”.当点D,E,P三点为“共生点”时,请直接写出 的值.