安徽省黄山市休宁县2020-2021学年九年级上学期数学第一次月考试卷
试卷更新日期:2020-12-05 类型:月考试卷
一、单选题
-
1. 下列交通标志既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2019年安徽经济运行总体平稳、稳中有进、进中向好,“十三五”规划经济总量目标提前一年实现,综合实力进一步提升.2019年全省全年生产总值超过37000亿元,将37000亿用科学记数法表示为( )A、 B、 C、 D、3. 方程x2=2x的根是( )A、0 B、2 C、0或2 D、无解4. 下列方程是关于 的一元二次方程的是( )A、 B、 C、 D、5. 由 平移得到抛物线 ,则下列平移过程正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向下平移2个单位 D、先向右平移1个单位,再向上平移2个单位6. 有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程正确的是( )A、 B、 C、 D、7. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
2. 2019年安徽经济运行总体平稳、稳中有进、进中向好,“十三五”规划经济总量目标提前一年实现,综合实力进一步提升.2019年全省全年生产总值超过37000亿元,将37000亿用科学记数法表示为( )A、 B、 C、 D、3. 方程x2=2x的根是( )A、0 B、2 C、0或2 D、无解4. 下列方程是关于 的一元二次方程的是( )A、 B、 C、 D、5. 由 平移得到抛物线 ,则下列平移过程正确的是( )A、先向左平移1个单位,再向上平移2个单位 B、先向左平移1个单位,再向下平移2个单位 C、先向右平移1个单位,再向下平移2个单位 D、先向右平移1个单位,再向上平移2个单位6. 有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程正确的是( )A、 B、 C、 D、7. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、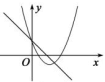 B、
B、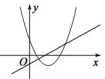 C、
C、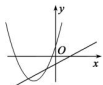 D、
D、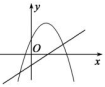 8. 某果园第1年水果产量为100吨,第3年水果产量为169吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x , 则根据题意可列方程为( )A、 B、 C、 D、9. 在函数① ② ③ 中,图象开口大小顺序用序号表示为( )A、①>②>③ B、①>③>② C、②>③>① D、②>①>③10. 如图,等腰 的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让 沿这条直线向右平移,直到点A与点E重合为止 设CD的长为x , 与正方形DEFG重合部分 图中阴影部分 的面积为y , 则y与x之间的函数关系的图象大致是( )
8. 某果园第1年水果产量为100吨,第3年水果产量为169吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x , 则根据题意可列方程为( )A、 B、 C、 D、9. 在函数① ② ③ 中,图象开口大小顺序用序号表示为( )A、①>②>③ B、①>③>② C、②>③>① D、②>①>③10. 如图,等腰 的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让 沿这条直线向右平移,直到点A与点E重合为止 设CD的长为x , 与正方形DEFG重合部分 图中阴影部分 的面积为y , 则y与x之间的函数关系的图象大致是( )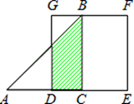 A、
A、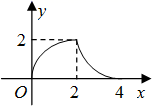 B、
B、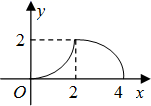 C、
C、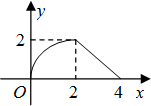 D、
D、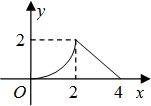
二、填空题
-
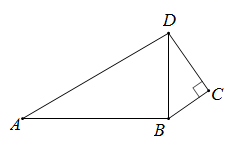
11. 函数y=x2﹣x﹣6的图象与x轴的交点坐标是12. 如图,已知∠C=90°,AB=12,BC=3,CD=4,AD=13,则∠ABD= .
 13. 已知抛物线y=﹣x2﹣2x+3,当﹣2≤x≤2时,对应的函数值y的取值范围为 .14. 若函数y=ax2+bx+c的图象经过P(1,0),Q(5,﹣4)当1≤x≤5时,y随x的增大而减小,则实数a的范围 .
13. 已知抛物线y=﹣x2﹣2x+3,当﹣2≤x≤2时,对应的函数值y的取值范围为 .14. 若函数y=ax2+bx+c的图象经过P(1,0),Q(5,﹣4)当1≤x≤5时,y随x的增大而减小,则实数a的范围 .三、解答题
-
15. 解一元二次方程:16. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
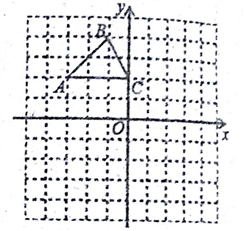 (1)、将△ABC以点C为旋转中心旋转180 ,画出旋转后对应的△A1B1C;(2)、平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;(3)、若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.17. 已知关于x的方程 .(1)、若该方程的一个根为1,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18.(1)、观察下列图形与等式的关系,并填空:
(1)、将△ABC以点C为旋转中心旋转180 ,画出旋转后对应的△A1B1C;(2)、平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;(3)、若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.17. 已知关于x的方程 .(1)、若该方程的一个根为1,求a的值及该方程的另一根;(2)、求证:不论a取何实数,该方程都有两个不相等的实数根.18.(1)、观察下列图形与等式的关系,并填空: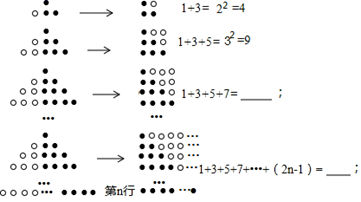 (2)、观察下图,根据 (1) 中结论,计算图中黑球的个数,用含有n的代数式填空:
(2)、观察下图,根据 (1) 中结论,计算图中黑球的个数,用含有n的代数式填空:
.
19. 如图,已知在 中, 分别是 的中点,连结 .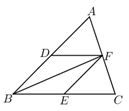 (1)、求证:四边形 是平行四边形;(2)、若 ,求四边形 的周长.20. 如图,二次函数的图象与x轴交于 和 两点,交y轴于点 ,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D .
(1)、求证:四边形 是平行四边形;(2)、若 ,求四边形 的周长.20. 如图,二次函数的图象与x轴交于 和 两点,交y轴于点 ,点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D . (1)、求二次函数的解析式;(2)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.21. 在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)、如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(1)、求二次函数的解析式;(2)、根据图象直接写出使一次函数值大于二次函数值的x的取值范围.21. 在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1 , A1B交AC于点E,A1C1分别交AC、BC于D、F两点.(1)、如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;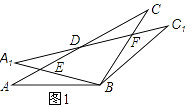 (2)、如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
(2)、如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.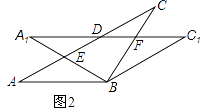 22. 某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价为25元/件时,每天的销售量是150件;销售单价每上涨1元,每天的销售量就减少10件.(1)、求商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大?(3)、现商场规定该文具每天销售量不少于120件,为使该文具每天的销售利润最大,该文具定价多少元时,每天利润最大?23. 如图,已知二次函数的图象经过点 、 和原点O . P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为 ,并与直线OA交于点C .
22. 某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价为25元/件时,每天的销售量是150件;销售单价每上涨1元,每天的销售量就减少10件.(1)、求商场销售这种文具每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、求销售单价为多少元时,该文具每天的销售利润最大?(3)、现商场规定该文具每天销售量不少于120件,为使该文具每天的销售利润最大,该文具定价多少元时,每天利润最大?23. 如图,已知二次函数的图象经过点 、 和原点O . P为二次函数图象上的一个动点,过点P作x轴的垂线,垂足为 ,并与直线OA交于点C .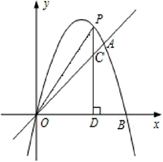 (1)、求出二次函数的解析式;(2)、当点P在直线OA的上方时,求线段PC的最大值;(3)、当点P在直线OA的上方时,求 的最大面积.
(1)、求出二次函数的解析式;(2)、当点P在直线OA的上方时,求线段PC的最大值;(3)、当点P在直线OA的上方时,求 的最大面积.