广西贵港高中2020-2021学年高二上学期理数期中教学质量监测试卷

试卷更新日期：2020-12-04 类型：期中考试

进入出卷网下载

一、单选题

1. 命题“若 $x = 1$ ，则 $x^{2} = 1$ ”的逆否命题是（）

A、若 $x^{2} = 1$ ，则 $x = 1$ B、若 $x \neq 1$ ，则 $x^{2} \neq 1$ C、若 $x = 1$ ，则 $x^{2} \neq 1$ D、若 $x^{2} \neq 1$ ，则 $x \neq 1$

查看试题解析
2. 命题“ $\forall x \in [0 ， + \infty) . x^{3} + x \geq 0$ ”的否定是（）

A、 $\forall x \in (- \infty ， 0) . x^{3} + x < 0$ B、 $\forall x \in (- \infty ， 0) . x^{3} + x \geq 0$ C、 $\exists x_{0} \in [0 ， + \infty) . x_{0}^{3} + x_{0} < 0$ D、 $\exists x_{0} \in [0 ， + \infty) . x_{0}^{3} + x_{0} \geq 0$

查看试题解析
3. 已知 $a \in R$ ，则“ $a > 1$ ”是“ $\frac{1}{a}$ ＜1”的（）

A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既非充分又非必要条件

查看试题解析
4. 已知正数m满足 $m^{2} - 2 m = 8$ ，则椭圆 $x^{2} + \frac{y^{2}}{m} = 1$ 的焦点坐标为（）

A、 $(\pm \sqrt{3}, 0)$ B、 $(0, \pm \sqrt{3})$ C、 $(\pm \sqrt{3}, 0)$ 或 $(\pm \sqrt{5}, 0)$ D、 $(0, \pm \sqrt{3})$ 或 $(\pm \sqrt{5}, 0)$

查看试题解析
5. 某学校从编号依次为001，002，…，900的900个学生中用系统抽样（等间距抽样）的方法抽取一个容量为20样本，已知样本中的有个编号为053，则样本中最大的编号为（）

A、853 B、854 C、863 D、864

查看试题解析
6. 如果在一次实验中，测得 $(x, y)$ 的四组数值分别是 $A (1, 3)$ ， $B (2, 3.8)$ ， $C (3, 5.2)$ ， $D (4, 6)$ ，则 $y$ 与 $x$ 之间的回归直线方程是（）

A、 $\hat{y} = x + 1.9$ B、 $\hat{y} = 1.04 x + 1.9$ C、 $\hat{y} = 0.95 x + 1.04$ D、 $\hat{y} = 1.05 x - 1.9$

查看试题解析
7. 6名同学到甲、乙、丙三个场馆做志愿者，每名同学只去1个场馆，甲场馆安排1名，乙场馆安排2名，丙场馆安排3名，则不同的安排方法共有（）

A、120种 B、90种 C、60种 D、30种

查看试题解析
8. 如图，大正方形的面积是13，四个全等的直角三角形围成一个小正方形.直角三角形的较短边长为2.向大正方形内投一飞镖，则飞镖落在小正方形内的概率为（）

A、 $\frac{1}{13}$ B、 $\frac{2}{13}$ C、 $\frac{3}{13}$ D、 $\frac{4}{13}$

查看试题解析
9. $(x + \frac{y^{2}}{x}) {(x + y)}^{5}$ 的展开式中x³y³的系数为（）

A、5 B、10 C、15 D、20

查看试题解析
10. 已知 $F_{1}$ ， $F_{2}$ 是椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左，右焦点， $A$ 是 $C$ 的左顶点，点 $P$ 在过 $A$ 且斜率为 $\frac{\sqrt{3}}{6}$ 的直线上， $△ P F_{1} F_{2}$ 为等腰三角形， $∠ F_{1} F_{2} P = 120 °$ ，则 $C$ 的离心率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
11. 已知函数 $f (x) = x^{2}$ ，函数 $g (x) = 2^{x} - a$ ，对 $\forall x_{1} \in [1, 5)$ 时，总 $\exists x_{2} \in [1, 5)$ 使得 $f (x_{1}) = g (x_{2})$ ，则 $a$ 的取值范围是（）

A、 $ϕ$ B、 $a \geq 7$ 或 $a \leq 1$ C、 $a > 7$ 或 $a < 1$ D、 $[1, 7]$

查看试题解析
12. 已知椭圆C的焦点为 $F_{1} (- 1 ， 0) ， F_{2} (1 ， 0)$ ，过F₂的直线与C交于A ， B两点.若 $│ A F_{2} │ = 2 │ F_{2} B │$ ， $│ A B │ = │ B F_{1} │$ ，则C的方程为（）

A、 $\frac{x^{2}}{2} + y^{2} = 1$ B、 $\frac{x^{2}}{3} + \frac{y^{2}}{2} = 1$ C、 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ D、 $\frac{x^{2}}{5} + \frac{y^{2}}{4} = 1$

查看试题解析

二、填空题

13. 已知 $(2 x^{2} + 3 x + 1) {(x - 2)}^{5} = a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{7} x^{7}$ ，求 $a_{0} + a_{1} + a_{2} + a_{3} + a_{4} + a_{5} + a_{6} + a_{7} =$

查看试题解析
14. 如图是一个算法流程图，若输出y的值为-2，则输入x的值是.

查看试题解析
15. 已知过点 $M (1, - 1)$ 的直线 $l$ 与椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ 相交于 $A, B$ 两点，若点 $M$ 是 $A B$ 的中点，则直线 $l$ 的方程为 .

查看试题解析
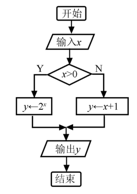16. 给出如下四个命题：①把二进制数 $110011_{(2)}$ 化为十进制数，结果为51；②将一组数据中的每个数据都加上或减去同一个常数后，平均值不变，方差不变；③从装有完全相同的4个红球和2个黄球的盒子中任取2个小球，则事件“至多一个红球”与“都是红球”互斥且对立；④若“ $p \land q$ ”为假命题，则 $p$ 、 $q$ 均为假命题.其中正确的命题的序号是．

查看试题解析

三、解答题

17. 为了解甲、乙两种离子在小鼠体内的残留程度，进行如下试验：将200只小鼠随机分成A，B两组，每组100只，其中A组小鼠给服甲离子溶液，B组小鼠给服乙离子溶液，每只小鼠给服的溶液体积相同、摩尔浓度相同。经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图：

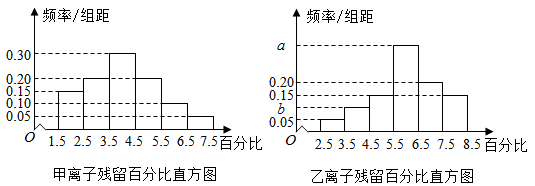
记C为事件：“乙离子残留在体内的百分比不低于5.5”，根据直方图得到P（C）的估计值为0.70.

(1)、求乙离子残留百分比直方图中a，b的值；

(2)、分别估计甲，乙离子残留百分比的平均值（同一组中的数据用该组区间的中点值为代表）

查看试题解析
18. 已知p：－x²＋6x＋16≥0，q：x²－4x＋4－m²≤0(m>0)．

(1)、若p为真，求实数x的取值范围；

(2)、若p是q成立的充分不必要条件，求实数m的取值范围．

查看试题解析
19. 已知平面内两定点 $M (- 1, 0), N (1, 0)$ ，动点 $P$ 满足 $| P M | + | P N | = 2 \sqrt{3}$ .

(1)、求动点 $P$ 的轨迹 $C$ 的方程；

(2)、若直线 $y = x + 1$ 与曲线C交于不同的两点 $A$ 、 $B$ ，求 $| A B |$ ．

查看试题解析
20. 某个体服装店经营各种服装，在某周内获纯利润 $y$ (元)与该周每天销售这种服装件数 $x$ 之间的一组数据关系如表：

$x$

3

4

5

6

7

8

9

$y$

66

69

73

81

89

90

91

参考数据及公式： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ． $\sum_{i = 1}^{7} x_{i}^{2} = 280, \sum_{i = 1}^{7} x_{i} y_{i} = 3487$ .

(1)、求 $\bar{x}$ ， $\bar{y}$ ；

(2)、若 $y$ 与 $x$ 线性相关，请求纯利润 $y$ 与每天销售件数 $x$ 间的回归直线方程.

查看试题解析
21. 随机抽取某中学甲乙两个班级各 $10$ 名同学，测量他们的身高(单位：cm)，获得的数据如下：
甲： $182 170 171 179 179 162 163 168 168 158$

乙： $181 170 173 176 178 179 162 165 168 159$

(1)、根据上述的数据作出茎叶图表示；

(2)、判断哪个班级的平均身高较高，并求出甲班的方差；

(3)、现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，则身高176cm的同学被抽中的概率是多少?

查看试题解析
22. 已知 $A$ ， $B$ 分别是椭圆 $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ 长轴的左，右顶点，点 $F$ 是椭圆的右焦点，点 $P$ 在椭圆上，且位于 $x$ 轴的上方，满足 $P A ⊥ P F$ ．

(1)、求点 $P$ 的坐标；

(2)、若线段 $A B$ 上的一点 $M$ 到直线 $A P$ 的距离等于 $| M B |$ ，求椭圆上的点到点 $M$ 的距离 $d$ 的最小值．

查看试题解析

$x$	3	4	5	6	7	8	9
$y$	66	69	73	81	89	90	91