2020-2021学年人教版数学六年级上学期 第八单元测试卷
试卷更新日期：2020-12-01 类型：单元试卷
一、选择题
-
1. 填在下面各正方形中的四个数之间都有相同的规律，根据此规律，m的值是（ ）。
A、38 B、52 C、66 D、742. 某餐厅里，一张桌子可坐6人，如图所示：
按照上面的规律，n张桌子能坐（ ）人。
A、6n+4 B、4n+4 C、4n+2 D、6n+63. 如下图，用火柴棒搭房子，搭三间用了13根。照这样计算，搭504间用（ ）根火柴棒。
A、2013 B、2015 C、20174. 有一组图，它的排列规律如下图，第7个图形由（ ）个
组成。 
A、21 B、25 C、28 D、325. 根据下图的规律，可知第⑥个图中有（ ）个。
A、21 B、25 C、296. 甜甜按照一定的规律用小棒摆出了下边的4幅图，如果按照这个规律继续摆，第6幅图要用的小棒根数是（ ）
A、31根 B、45根 C、57根 D、63根7. “数形结合”是一种数学思想方法，通过数与形之间的对应关系，体现抽象思维与形象思维的结合。下图的图形对应的算式是（ ）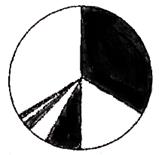
A、 B、 C、 D、都不对8. 把一些规格相同的杯子叠起来（如图），4个杯子叠起来高20厘米，6个杯子叠起来高26厘米。n个杯子叠起来的高度可以用下面（ ）的关系式来表示。
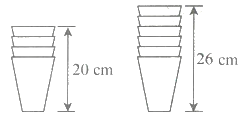A、6n-10 B、3n+11 C、6n-4 D、3n+89. 将一些小圆球如下图摆放，第六幅图有（ ）个小圆球。
A、30 B、42 C、48 D、5610. 根据图中的信息，第六个图案所对应的式子是（ ）
A、7＋1 B、62＋1 C、72＋1 D、82＋1二、判断题
-
11. 摆1个正方形需要4根小棒，往后每多摆1个正方形就增加3根小棒，按这样的规律摆10个正方形，一共需要31根小棒．（判断对错）12.
…，第五个点阵中点的个数是1+4×5=21． 三、填空题
-
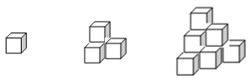
13. 给某环形道种了2012棵树，如果从某一棵开始，每隔5棵树挂一盏彩灯，依次绕圈挂下去，一共挂了2012盏彩灯。那么恰好挂有两盏彩灯的树有棵。14. 有若干个棱长为1厘米的小正方体，如果把这些小正方体按如图所示的方式放置，当放置5层时，放置成的物体的表面积是平方厘米。
15. 自主探索。
仔细观察上面的点子图，根据每个图中点子的排列规律，想一想，可以怎样计算每个图中点子的总个数?请你把下表填写完整。
序号
1
2
3
4
…
表示点子数的算式
1
1+4
…
点子的总个数
1
5
…
观察表中数据，如果用A表示第n个图形中点子的个数，A和n之间的关系可以表示成：
A= 。
16. 观察下图，每个图形中间是白色小正方形，周围是灰色小正方形。
照这样画下去，第10个图形中有个白色小正方形，个灰色小正方形。
17. 右图是一组有规律的图案，第1个图案是由4个基本图形组成，第2个图案是由7个基本图形组成，……则第5个图案是由个基本图形组成。
18. 摆一摆，找规律。
摆第7个图形需要根小棒，摆第n个图形需要根小棒。
19. 观察下图，照规律摆下去，第6个图中有个黑色方块，第n个图中有个黑色方块。
20. 用黑、白两种正方形的瓷砖拼成大的正方形图形，要求中间用白瓷砖，四周一圈用黑瓷砖。（如图所示）如果所拼的图形中用了400块白瓷砖，那么黑瓷砖用了块；如果所拼的图形中用了400块黑瓷砖，那么白瓷砖用了块。
21. 依据图中的规律，在括号内填上适当的分数。
22. 如图是按规律排列的三角形数阵：第1行：（1）；
第2行：（1，1）；
第3行：（1，2，1）；……
第2020行左起第三个数与左起第二个数的比的比值为.
四、解答题
-
23. 下图中的数是“三角形数”。先观察图形，再完成练习。
(1)、照样子画一画，并在括号里写出这个“三角形数”。(2)、第1个“三角形数”：1；第2个“三角形数”：1+2；第3个“三角形数”：1+2+3；……第n个“三角形数”：。24. 25是一个“正方形数”，下面表示25的不同构造方法中，分别可以用哪个算式表示?选一选，填一填。
① 25 = 52
②25=1+3+5+7+9
③25=5+4+4+3+3+2+2+1+1
④25=1+2+3+4+5+4+3+2+1
25. 探索与发现意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1、1、2、3、5、8、13……计算 这样的算式时有简便方法吗？
丁丁遇到这个问题时，想到用“数形结合”的方法来探索，于是他以这组数中各个数作为正方形的边长构造成正方形，再拼成如图所示的长方形来研究。
图形
…
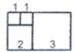
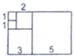
算式
…
序号
①
②
③
④
…
(1)、观察上面的图形和算式，你能把下面算式补充完整吗？(2)、若按此规律继续拼长方形，则序号为的长方形面积数是714.