四川成都新都区四中2020-2021学年八年级上学期数学9月月考试卷
试卷更新日期:2020-12-01 类型:月考试卷
一、单选题
-
1. 下列各组数中能构成直角三角形的是( )A、3,4,7 B、 C、4, 6, 8, D、9, 40 , 412. 在实数0.3,0, , ,0.123456…^87.654345454545……中,其中无理数的个数是( )A、2 B、3 C、4 D、53. 下列计算中,正确的是( )A、 B、 C、 D、4. 如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了( )
 A、2cm B、3cm C、4cm D、5cm5. 如图,∠A=∠D=90°,AC与BD相交于点O,AB=CD=4,AO=3,则BD的长为( )
A、2cm B、3cm C、4cm D、5cm5. 如图,∠A=∠D=90°,AC与BD相交于点O,AB=CD=4,AO=3,则BD的长为( ) A、6 B、7 C、8 D、106. 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为( )
A、6 B、7 C、8 D、106. 如图,在三角形纸片ABC中,∠C=90°,AC=18,将∠A沿DE折叠,使点A与点B重合,折痕和AC交于点E,EC=5,则BC的长为( ) A、9 B、12 C、15 D、187. 4 、 、15三个数的大小关系是( )A、 4 <15< B、 <15<4 C、4 < <15 D、 <4 <158. 的三边长分别为 ,下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的个数有( )A、1个 B、2个 C、3个 D、4个9. 设a=20 , b=(-3)2 , c= ,d= ,则 , , , 按由小到大的顺序排列正确的是( )A、c<a<d<b B、b<d<a<c C、a<c<d<b D、b<c<a<d10. 如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边长分别为6m和8m,按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A、9 B、12 C、15 D、187. 4 、 、15三个数的大小关系是( )A、 4 <15< B、 <15<4 C、4 < <15 D、 <4 <158. 的三边长分别为 ,下列条件:① ;② ;③ ;④ .其中能判断 是直角三角形的个数有( )A、1个 B、2个 C、3个 D、4个9. 设a=20 , b=(-3)2 , c= ,d= ,则 , , , 按由小到大的顺序排列正确的是( )A、c<a<d<b B、b<d<a<c C、a<c<d<b D、b<c<a<d10. 如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边长分别为6m和8m,按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( ) A、2m B、3m C、6m D、9m
A、2m B、3m C、6m D、9m二、填空题
-
11. 的算术平方根是 . 的倒数是 .12. 若 ,则x的取值范围是 .13. 如图所示,在边长为1个单位长度的小正方形组成的网格中,点A.B都是格点,则线段AB的长度为 .
 14. 三角形三条边长分别为8,15,17,那么最短边上的高是 .15. 当 时, .16. 完成下列各题,(1)、若 ,那么 的值是 .(2)、化简: .17. 如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .
14. 三角形三条边长分别为8,15,17,那么最短边上的高是 .15. 当 时, .16. 完成下列各题,(1)、若 ,那么 的值是 .(2)、化简: .17. 如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .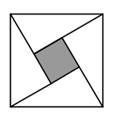 18. 如图,△ACB和△ECD都是等腰直角三角形,△ACB的锐角顶点A在△ECD的斜边DE上,若AE= ,AC= ,则DE=.
18. 如图,△ACB和△ECD都是等腰直角三角形,△ACB的锐角顶点A在△ECD的斜边DE上,若AE= ,AC= ,则DE=. 19. 已知直角三角形两边长 、 满足 ,则第三边长为 .
19. 已知直角三角形两边长 、 满足 ,则第三边长为 .三、解答题
-
20. 化简(1)、 .(2)、 .(3)、 .(4)、 .21. 解方程(1)、 .(2)、 .22. 的小数部分为 , 的小数部分为 ,求:(1)、a+b的值.(2)、a-b的值.(3)、 的值.23. 确定合适的数轴,在数轴上画出表示 的点 和表示 的点 .24. 如图,圆柱底面半径为 ,高为 ,点 、 分别是圆柱两底面圆周上的点,且 、 在同一母线上,用一根棉线从 点顺着圆柱侧面绕3圈到 点,求这根棉线的长度最短.
 25. 如图, 是等腰 内一点, ,连接 , , .
25. 如图, 是等腰 内一点, ,连接 , , . 图1
图1 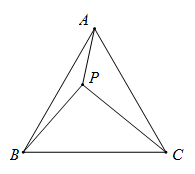 图2(1)、如图1,当 时, , , ,求 .(2)、如图2,当 时, , , ,求 .
图2(1)、如图1,当 时, , , ,求 .(2)、如图2,当 时, , , ,求 .

