福建省厦门市北师大附校2020-2021学年九年级上学期数学10月月考试卷

试卷更新日期：2020-12-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 在四个数 $\sqrt{3}$ ， $\sqrt{2}$ ，1.7，2中，最大的是（）

A、 $\sqrt{3}$ B、 $\sqrt{2}$ C、1.7 D、2

查看试题解析
2. 已知一个一元二次方程的二次项系数是3，常数项是1，则这个一元二次方程可能是（）

A、3x+1=0 B、x²+3=0 C、3x²﹣1=0 D、3x²+6x+1=0

查看试题解析
3. 方程 ${(x - 1)}^{2} = 0$ 的根是（）

A、 $x_{1} = x_{2} = 1$ B、 $x_{1} = 1$ ， $x_{2} = 0$ C、 $x_{1} = - 1$ ， $x_{2} = 0$ D、 $x_{1} = 1$ ， $x_{2} = - 1$

查看试题解析
4. 一元二次方程x²﹣2x﹣5=0根的判别式的值是（）

A、24 B、16 C、﹣16 D、﹣24

查看试题解析
5. 下列运算正确的是（）

A、 $3 a^{2} - a^{2} = 3$ B、 ${(a + b)}^{2} = a^{2} + b^{2}$ C、 ${(- 3 a b^{2})}^{2} = - 6 a^{2} b^{4}$ D、 $a \cdot a^{- 1} = 1 (a \neq 0)$

查看试题解析
6. 抛物线y=2（x﹣2）²+5向左平移3个单位长度，再向下平移2个单位长度，此时抛物线的对称轴是（）

A、x=2 B、x=﹣1 C、x=5 D、x=0

查看试题解析
7. 已知 $(3 - \sqrt{5}) \cdot a = b$ ，若b是整数，则a的值可能是（）

A、 $\sqrt{5}$ B、 $3 - \sqrt{5}$ C、 $6 + 2 \sqrt{5}$ D、3

查看试题解析
8. 已知抛物线 $y = a x^{2} + b x + c$ 和 $y = n a x^{2} + n b x + n c$ ，其中a ， b ， c ， n均为正数，且 $n \neq 1$ ，则关于这两条抛物线，下列判断正确的是（）

A、顶点的纵坐标相同 B、对称轴相同 C、与y轴的交点相同 D、其中一条经过平移可以与另一条重合

查看试题解析
9. 已知甲、乙两个函数图象上的部分点的横坐标x与纵坐标y如表所示．若在实数范围内，甲、乙的函数值都随自变量的增大而减小，且两个图象只有一个交点，则关于这个交点的横坐标a ，下列判断正确的是（）

x

﹣2

0

2

4

y_甲

5

4

3

2

y_乙

6

5

3.5

0

A、a＜﹣2 B、﹣2＜a＜0 C、0＜a＜2 D、2＜a＜4

查看试题解析
10. 某药厂2013年生产1t甲种药品的成本是6000元.随着生产技术的进步，2015年生产1t甲种药品的成本是3600元.设生产1t甲种药品成本的年平均下降率为x，则x的值是（）

A、 $\frac{5 - \sqrt{15}}{5}$ B、 $\frac{5 + \sqrt{15}}{5}$ C、 $\frac{\sqrt{15}}{5}$ D、 $\frac{2}{5}$

查看试题解析

二、填空题

11. 已知x＝1是方程x²﹣a＝0的根，则a＝．

查看试题解析
12. 若关于x的一元二次方程 $x^{2} - 4 x + c = 0$ 有两个相等的实数根，则c的值是.

查看试题解析
13. 当 $x =$ 时，二次函数 $y = 2 {(x - 3)}^{2} - 5$ 的最小值是．

查看试题解析
14. 把小圆形场地的半径增加5米得到大圆形场地，此时大圆形场地的面积是小圆形场地的4倍，设小圆形场地的半径为x米，若要求出未知数x，则应列出方程（列出方程，不要求解方程）．

查看试题解析
15. 已知▱ABCD的顶点B（1，1），C（5，1），直线BD ， CD的解析式分别是y＝kx ， y＝mx﹣14，则BC＝，点A的坐标是．

查看试题解析
16. 已知 a - b=2, ab +2b - c $^{2}$ + 2c= 0，当 b≥0,-2≤c< 1 ，整数 a 的值是 .

查看试题解析

三、解答题

17.

(1)、计算： $\sqrt{6} \times \sqrt{3} - \sqrt{12} + \sqrt{2}$

(2)、解方程： $x^{2} + 4 x - 1 = 0$

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
19. 已知二次函数 $y = x^{2} + b x + c$ 的图像经过点A（0，3），B（-1，0）.

(1)、求该二次函数的解析式

(2)、在图中画出该函数的图象

查看试题解析
20. 如图，利用一面长度为7米的墙，用20米长的篱笆能否围出一个面积为48平方米的矩形菜园？若能，求出该菜园与墙平行一边的长度；若不能，说明理由．

查看试题解析
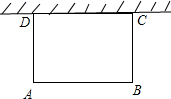21. 在正方形ABCD中，E是CD边上的点，过点E作EF⊥BD于F．

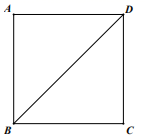(1)、尺规作图：在图中求作点E，使得EF=EC；(保留作图痕迹，不写作法)

(2)、在(1)的条件下，连接FC，求∠BCF的度数．

查看试题解析
22. 阅读下列材料
我们通过下列步骤估计方程2x²+x﹣2=0的根的所在的范围．

第一步：画出函数y=2x²+x﹣2的图象，发现图象是一条连续不断的曲线，且与x轴的一个交点的横坐标在0，1之间．

第二步：因为当x=0时，y=﹣2＜0；当x=1时，y=1＞0．

所以可确定方程2x²+x﹣2=0的一个根x₁所在的范围是0＜x₁＜1．

第三步：通过取0和1的平均数缩小x₁所在的范围；

取x= $\frac{0 + 1}{2} = \frac{1}{2}$ ，因为当x= $\frac{1}{2}$ 时，y＜0，

又因为当x=1时，y＞0，

所以 $\frac{1}{2}$ ＜x₁＜1．

(1)、请仿照第二步，通过运算，验证2x²+x﹣2=0的另一个根x₂所在范围是﹣2＜x₂＜﹣1；

(2)、在﹣2＜x₂＜﹣1的基础上，重复应用第三步中取平均数的方法，将x₂所在范围缩小至m＜x₂＜n，使得n﹣m≤ $\frac{1}{4}$ ．

查看试题解析
23. 已知 $A (m_{1}, n_{1})$ ， $B (m_{2}, n_{2})$ $(m_{1} < m_{2})$ 在直线 $y = k x + b$ 上．

(1)、若点A（-2，1），B（1，2），求直线AB的解析式；

(2)、若 $m_{1} + m_{2} = 3 b$ ， $n_{1} + n_{2} = k b + 4$ ， $b > 2$ ．试比较 $n_{1}$ 和 $n_{2}$ 的大小，并说明理由．

查看试题解析
24. 如图，直线l： $y = - 3 x + 3$ 与x轴、y轴分别相交于A、B两点，抛物线 $y = a x^{2} - 2 a x + a + 4 (a < 0)$ 经过点B ．

(1)、求该抛物线的函数表达式：

(2)、已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM ，设点M的横坐标为m ， △ABM的面积为S ，求S与m的函数表达式，并求出S的最大值．

查看试题解析
25. 已知抛物线 $y = x^{2} - 2 m x + m^{2} + 2 m - 2$ ，直线 $l_{1} : y = x + m$ ，直线 $l_{2} : y = x + m + b$

(1)、当m=0时，若直线 $l_{2}$ 经过此抛物线的顶点，求b的值

(2)、将此抛物线夹在 $l_{1} 与 l_{2}$ 之间的部分（含交点）图象记为 $C$ ，若 $- \frac{3}{2} < b < 0$ ，
①判断此抛物线的顶点是否在图象 $C$ 上，并说明理由；

②图象 $C$ 上是否存在这样的两点： $M (a_{1}, b_{1}) 和 N (a_{2}, b_{2})$ ，其中 $a_{1} \neq a_{2}, b_{1} \neq b_{2}$ ？若存在，求相应的 $m$ 和 $b$ 的取值范围

查看试题解析

x	﹣2	0	2	4
y_甲	5	4	3	2
y_乙	6	5	3.5	0