福建省龙岩市永定区金丰片2020-2021学年八年级上学期数学第一次月考试卷
试卷更新日期：2020-12-01 类型：月考试卷
一、单选题
-
1. 下列图形中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 将下列长度的三根木棒首尾顺次相接，能组成三角形的是（ ）
A、1cm，2cm，3cm B、2cm，2cm，4cm C、3cm，4cm，12cm D、4cm，5cm，6cm3. 若一个多边形的内角和为1080°，则这个多边形的边数为（）
A、6 B、7 C、8 D、94. 如图，以正方形ABCD的中心为原点建立平面直角坐标系，点A的坐标为（2，2），则点C的坐标为（ ）
A、（2，2） B、（﹣2，2） C、（﹣2，﹣2） D、（2，﹣2）5. 如图，用三角尺可按下面的方法画角平分线：在∠AOB的两边上，分别取OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP，通过证明△OMP≌△ONP可以说明OP是∠AOB的角平分线，那么△OMP≌△ONP的依据是（ ）
A、SSS B、SAS C、AAS D、HL6. 如图，若 MB = ND ， ∠MBA = ∠NDC ， 下列条件中不能判定△ABM ≌△CDN 的是（ ）
A、AM = CN B、AM //CN C、AB = CD D、∠M = ∠N7. 将一副三角板按如图所示摆放，图中∠α的度数是（ ）
A、75° B、90° C、105° D、120°8. 如图，Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5，AD平分∠BAC．则S△ACD：S△ABD=（ ）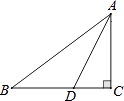
A、3：4 B、3：5 C、4：5 D、1：19. 如图，把矩形 沿 对折后使两部分重合，若 ，则 =（ ）
A、110° B、115° C、120° D、130°10. 坐标平面内一点A（1，2），O是原点，P是x轴上一个动点，如果以点P、O、A为顶点的三角形为等腰三角形，那么符合条件的动点P的个数为（ ）A、1 B、2 C、3 D、4二、填空题
-
11. 工人师傅在做完门框后，为防止变形，经常如图所示钉上两根斜拉的木条（即图中的AB、CD两根木条），这样做的数学原理是： ．
12. 在△ABC中，∠B=50°，∠C=60°，则∠A的度数是度.13. 等腰三角形的两边长分别是3和7，则其周长为 ．14. 如图，ΔABC与ΔA′B′C′关于直线l对称，则∠B的度数为 ．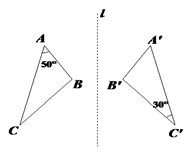
15. 如图，△ABC的三边AB，AC，BC的长分别为4，6，8，其三条角平分线将△ABC分成三个三角形，则S△OAB∶S△OAC∶S△OBC＝ ．
16. 如图，在△ABC中，E为AC的中点，点D为BC上一点，BD：CD=2：3，AD、BE交于点O，若S△AOE﹣S△BOD=1，则△ABC的面积为 ．
三、解答题
-
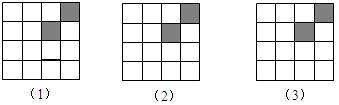
17. 一个多边形的内角和是它的外角和的4倍，求这个多边形的边数．18. 如图是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑，请你用三种不同的方法分别在下图中再涂黑三个空白的小正方形，使它成为轴对称图形．
19. 如图，在△ABC中，AB＝AC，BD＝CD，求证：△ABD≌△ACD．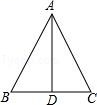
20. 如图，早上8：00，一艘轮船以15海里/小时的速度由南向北航行，在A处测得小岛P在北偏西15°方向上，到上午10：00，轮船在B处测得小岛P在北偏西30°方向上，在小岛P周围18海里内有暗礁，若轮船继续向前航行，有无触礁的危险？
21. 已知，△ABC在平面直角坐标系中的位置如图所示．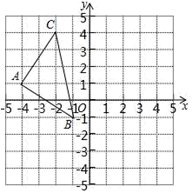
(1)、请画出△ABC关于y轴对称的 ．(2)、求△ABC的面积．22. 求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形（请画出图形，写出已知、求证、证明的过程）．23. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=30°．
(1)、求∠BAE的度数；(2)、求∠DAE的度数；(3)、探究：小明认为如果只知道∠B﹣∠C=40°，也能得出∠DAE的度数？你认为可以吗？若能，请你写出求解过程；若不能，请说明理由．24. 如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交AC于M．
(1)、若∠B=70°，则∠NMA的度数是 ．(2)、连接MB，若AB=8cm，△MBC的周长是14cm．①求BC的长；
②在直线MN上是否存在点P，使由P，B，C构成的△PBC的周长值最小？若存在，标出点P的位置并求△PBC的周长最小值；若不存在，说明理由．
25. 如图，在长方形ABCD中，AB＝CD＝6cm ， BC＝10cm ， 点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：
(1)、PC＝cm ． （用t的代数式表示）(2)、当t为何值时，△ABP≌△DCP？(3)、当点P从点B开始运动，同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由．