2016年浙江省金华市中考数学试卷
试卷更新日期:2016-06-21 类型:中考真卷
一、选择题
-
1. 实数﹣ 的绝对值是( )A、2 B、 C、﹣ D、﹣2.
若实数a,b在数轴上的位置如图所示,则下列判断错误的是( )
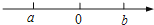 A、a<0 B、ab<0 C、a<b D、a,b互为倒数3.
A、a<0 B、ab<0 C、a<b D、a,b互为倒数3.如图是加工零件的尺寸要求,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
 A、Φ45.02 B、Φ44.9 C、Φ44.98 D、Φ45.014.
A、Φ45.02 B、Φ44.9 C、Φ44.98 D、Φ45.014.从一个边长为3cm的大立方体挖去一个边长为1cm的小立方体,得到的几何体如图所示,则该几何体的左视图正确的是( )
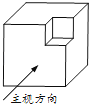 A、
A、 B、
B、 C、
C、 D、
D、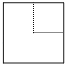 5. 一元二次方程x2﹣3x﹣2=0的两根为x1 , x2 , 则下列结论正确的是( )A、x1=﹣1,x2=2 B、x1=1,x2=﹣2 C、x1+x2=3 D、x1x2=26.
5. 一元二次方程x2﹣3x﹣2=0的两根为x1 , x2 , 则下列结论正确的是( )A、x1=﹣1,x2=2 B、x1=1,x2=﹣2 C、x1+x2=3 D、x1x2=26.如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD的是( )
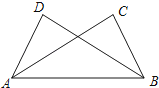 A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD7. 小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )A、 B、 C、 D、8.
A、AC=BD B、∠CAB=∠DBA C、∠C=∠D D、BC=AD7. 小明和小华参加社会实践活动,随机选择“打扫社区卫生”和“参加社会调查”其中一项,那么两人同时选择“参加社会调查”的概率为( )A、 B、 C、 D、8.一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度1米,则地毯的面积至少需要( )
 A、 米2 B、 米2 C、(4+ )米2 D、(4+4tanθ)米29.
A、 米2 B、 米2 C、(4+ )米2 D、(4+4tanθ)米29.足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.如图的正方形网格中,点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,最好的射点在( )
 A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点10.
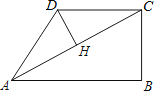
A、点C B、点D或点E C、线段DE(异于端点) 上一点 D、线段CD(异于端点) 上一点10.在四边形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,点H为垂足.设AB=x,AD=y,则y关于x的函数关系用图象大致可以表示为( )
 A、
A、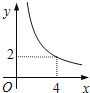 B、
B、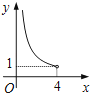 C、
C、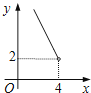 D、
D、
二、填空题
-
11. 不等式3x+1<﹣2的解集是 .12. 能够说明“ =x不成立”的x的值是(写出一个即可).13.
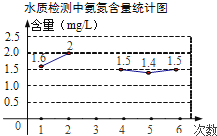
为监测某河道水质,进行了6次水质检测,绘制了如图的氨氮含量的折线统计图.若这6次水质检测氨氮含量平均数为1.5mg/L,则第3次检测得到的氨氮含量是mg/L.
 14.
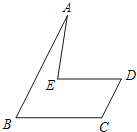
14.如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
 15.
15.如图,Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC 上,以AD为折痕△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .
 16.
16.由6根钢管首尾顺次铰接而成六边形钢架ABCDEF,相邻两钢管可以转动.已知各钢管的长度为AB=DE=1米,BC=CD=EF=FA=2米.(铰接点长度忽略不计)
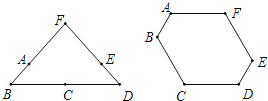 (1)、转动钢管得到三角形钢架,如图1,则点A,E之间的距离是米.(2)、转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是米.
(1)、转动钢管得到三角形钢架,如图1,则点A,E之间的距离是米.(2)、转动钢管得到如图2所示的六边形钢架,有∠A=∠B=∠C=∠D=120°,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是米.三、解答题
-
17. 计算: ﹣(﹣1)2016﹣3tan60°+(﹣2016)0 .18. 解方程组 .19.
某校组织学生排球垫球训练,训练前后,对每个学生进行考核.现随机抽取部分学生,统计了训练前后两次考核成绩,并按“A,B,C”三个等次绘制了如图不完整的统计图.试根据统计图信息,解答下列问题:
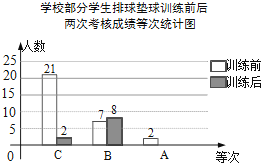 (1)、抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.(2)、若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.20.
(1)、抽取的学生中,训练后“A”等次的人数是多少?并补全统计图.(2)、若学校有600名学生,请估计该校训练后成绩为“A”等次的人数.20.如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
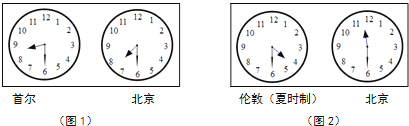 (1)、设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).
(1)、设北京时间为x(时),首尔时间为y(时),就0≤x≤12,求y关于x的函数表达式,并填写下表(同一时刻的两地时间).北京时间
7:30
11:15
2:50
首尔时间
8:30
12:15
3:50
(2)、如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为7:30,那么此时韩国首尔时间是多少?21.如图,直线y= x﹣ 与x,y轴分别交于点A,B,与反比例函数y= (k>0)图象交于点C,D,过点A作x轴的垂线交该反比例函数图象于点E.
 (1)、求点A的坐标.(2)、若AE=AC.
(1)、求点A的坐标.(2)、若AE=AC.①求k的值.
②试判断点E与点D是否关于原点O成中心对称?并说明理由.
22.四边形ABCD的对角线交于点E,有AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
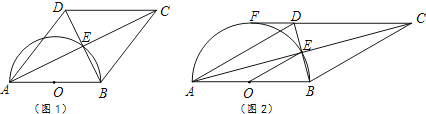 (1)、利用图1,求证:四边形ABCD是菱形.(2)、如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.
(1)、利用图1,求证:四边形ABCD是菱形.(2)、如图2,若CD的延长线与半圆相切于点F,已知直径AB=8.①连结OE,求△OBE的面积.
②求弧AE的长.
23.在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.
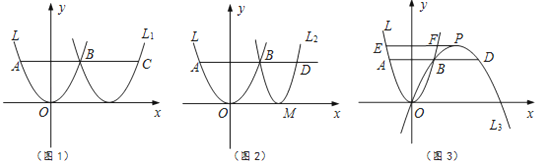 (1)、已知a=1,点B的纵坐标为2.
(1)、已知a=1,点B的纵坐标为2.①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD= AB,过点B,D的抛物线L2 , 其顶点M在x轴上,求该抛物线的函数表达式.
(2)、如图3,若BD=AB,过O,B,D三点的抛物线L3 , 顶点为P,对应函数的二次项系数为a3 , 过点P作PE∥x轴,交抛物线L于E,F两点,求 的值,并直接写出 的值.
24.在平面直角坐标系中,点O为原点,点A的坐标为(﹣6,0).如图1,正方形OBCD的顶点B在x轴的负半轴上,点C在第二象限.现将正方形OBCD绕点O顺时针旋转角α得到正方形OEFG.
 (1)、如图2,若α=60°,OE=OA,求直线EF的函数表达式.(2)、若α为锐角,tanα= ,当AE取得最小值时,求正方形OEFG的面积.(3)、当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为 :1?若能,求点P的坐标;若不能,试说明理由
(1)、如图2,若α=60°,OE=OA,求直线EF的函数表达式.(2)、若α为锐角,tanα= ,当AE取得最小值时,求正方形OEFG的面积.(3)、当正方形OEFG的顶点F落在y轴上时,直线AE与直线FG相交于点P,△OEP的其中两边之比能否为 :1?若能,求点P的坐标;若不能,试说明理由