2016年四川省自贡市中考数学试卷
试卷更新日期:2016-06-21 类型:中考真卷
一、选择题
-
1. 计算1﹣(﹣1)的结果是( )A、2 B、1 C、0 D、﹣22. 将0.00025用科学记数法表示为( )A、2.5×104 B、0.25×10﹣4 C、2.5×10﹣4 D、25×10﹣53. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、4. 把a2﹣4a多项式分解因式,结果正确的是( )A、a(a﹣4) B、(a+2)(a﹣2) C、a(a+2)(a﹣2) D、(a﹣2)2﹣45.
如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
 A、15° B、25° C、30° D、75°6. 若 +b2﹣4b+4=0,则ab的值等于( )A、﹣2 B、0 C、1 D、27. 已知关于x的一元二次方程x2+2x﹣(m﹣2)=0有实数根,则m的取值范围是( )A、m>1 B、m<1 C、m≥1 D、m≤18.
A、15° B、25° C、30° D、75°6. 若 +b2﹣4b+4=0,则ab的值等于( )A、﹣2 B、0 C、1 D、27. 已知关于x的一元二次方程x2+2x﹣(m﹣2)=0有实数根,则m的取值范围是( )A、m>1 B、m<1 C、m≥1 D、m≤18.如图是几何体的俯视图,所表示数字为该位置小正方体的个数,则该几何体的正视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 9. 圆锥的底面半径为4cm,高为5cm,则它的表面积为( )A、12πcm2 B、26πcm2 C、πcm2 D、(4 +16)πcm210.
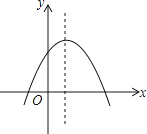
9. 圆锥的底面半径为4cm,高为5cm,则它的表面积为( )A、12πcm2 B、26πcm2 C、πcm2 D、(4 +16)πcm210.二次函数y=ax2+bx+c的图象如图,反比例函数y= 与正比例函数y=bx在同一坐标系内的大致图象是( )
 A、
A、 B、
B、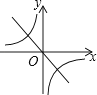 C、
C、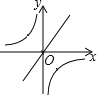 D、
D、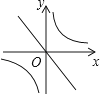
二、填空题
-
11. 若代数式 有意义,则x的取值范围是 .12. 若n边形内角和为900°,则边数n= .13.
一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是 .
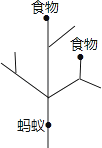 14.
14.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x﹣6上时,线段BC扫过的面积为cm2 .
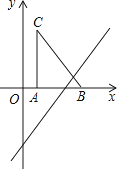 15.
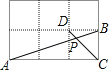
15.如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB,CD相交于点P,则 的值= , tan∠APD的值= .
三、解答题
-
16. 计算:( )﹣1+(sin60°﹣1)0﹣2cos30°+| ﹣1|17. 解不等式组 .请结合题意填空,完成本题的解答.(1)、解不等式①,得:;(2)、解不等式②,得:;(3)、
把不等式①和②的解集在数轴上表示出来;
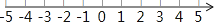 (4)、不等式组的解集为: .18. 某校为了丰富大家的业余生活,组织了一次工会活动,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为奖品,若购买2支钢笔和3本笔记本共需62元,5支钢笔和1本笔记本共需90元,问购买一支钢笔和一本笔记本各需多少元?19.
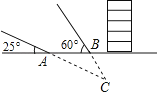
(4)、不等式组的解集为: .18. 某校为了丰富大家的业余生活,组织了一次工会活动,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为奖品,若购买2支钢笔和3本笔记本共需62元,5支钢笔和1本笔记本共需90元,问购买一支钢笔和一本笔记本各需多少元?19.某国发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作,如图,某探测对在地面A、B两处均探测出建筑物下方C处由生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米,参考数据:sin25°≈0.4,cos25°≈0,9,tan25°≈0.5, ≈1.7)
 20.
20.我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
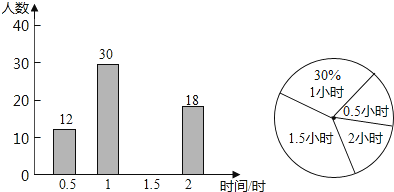 (1)、将条形统计图补充完整;(2)、扇形图中的“1.5小时”部分圆心角是多少度?(3)、求抽查的学生劳动时间的众数、中位数.21.
(1)、将条形统计图补充完整;(2)、扇形图中的“1.5小时”部分圆心角是多少度?(3)、求抽查的学生劳动时间的众数、中位数.21.如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.
 (1)、求证:∠1=∠BAD;(2)、求证:BE是⊙O的切线.22.
(1)、求证:∠1=∠BAD;(2)、求证:BE是⊙O的切线.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y= 的图象的两个交点.
 (1)、求一次函数和反比例函数的解析式;(2)、观察图象,直接写出方程kx+b﹣ =0的解;(3)、求△AOB的面积;(4)、观察图象,直接写出不等式kx+b﹣ <0的解集.23.
(1)、求一次函数和反比例函数的解析式;(2)、观察图象,直接写出方程kx+b﹣ =0的解;(3)、求△AOB的面积;(4)、观察图象,直接写出不等式kx+b﹣ <0的解集.23.已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处
 (1)、如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.(2)、如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.24.
(1)、如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.(2)、如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.24.抛物线y=﹣x2+4ax+b(a>0)与x轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
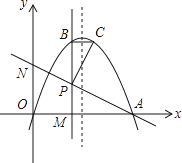 (1)、a= 时,求抛物线的解析式和BC的长;(2)、如图a>1时,若AP⊥PC,求a的值.
(1)、a= 时,求抛物线的解析式和BC的长;(2)、如图a>1时,若AP⊥PC,求a的值.